9.8. Докажите, что значение выра переменной: 1) ((n'))4 : (n')2-5-n10; 3) ((a')) - a' + 19 - (a²)³; шопие. от значения 2) m30 : ((m³)2)³ + 17 - (m³)2; 4)-23-b4⁰ + ((b5)4)².
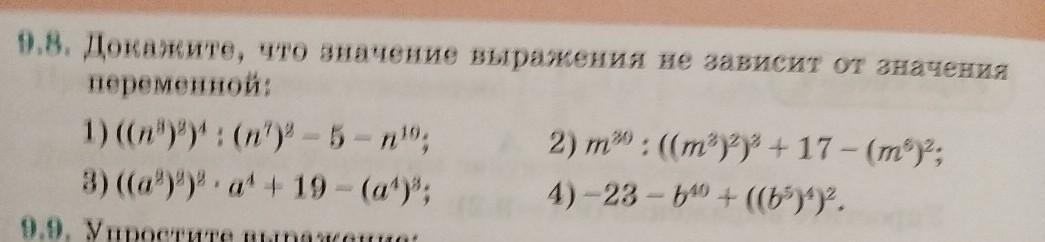
Ответы
Ответ:
Для спрощення виразу підставимо дані значення:
((n'))⁴ : (n')² - 5 - n¹⁰
Так як n' означає "n піднесене до ступеня 1", то ((n'))⁴ = (n¹)⁴ = n⁴.
(n')² означає "n піднесене до ступеня 2", то (n')² = (n¹)² = n².
Заміняючи ці значення в виразі, ми отримуємо:
n⁴ : n² - 5 - n¹⁰
Тепер ми можемо спростити вираз, ділячи n⁴ на n², що дає n²:
n² - 5 - n¹⁰
Це є остаточним значенням виразу.
Знову ж таки, щоб знайти значення виразу m³⁰ : ((m³)²)³ + 17 - (m³)², спростимо вираз, замінивши m³⁰ на 1, оскільки будь-яке число, піднесене до ступеня 0, дорівнює 1:
1 : ((m³)²)³ + 17 - (m³)²
Тепер розглянемо (m³)². Це означає "m піднесене до ступеня 3, піднесене до ступеня 2", а отже, (m³)² = (m^(3*2)) = m⁶.
Підставимо це значення в вираз:
1 : (m⁶)³ + 17 - m⁶
Знову ж таки, ми можемо спростити вираз, піднімаючи m⁶ до куба, що дає m^(6*3) = m¹⁸:
1 : m¹⁸ + 17 - m⁶
Це є остаточним значенням виразу.
Для спрощення виразу ((a')) - a' + 19 - (a²)³, спростимо ((a')) до a¹ (оскільки a' означає "a піднесене до ступеня 1"):
a¹ - a' + 19 - (a²)³
Тепер розглянемо (a²)³. Це означає "a піднесене до ступеня 2, піднесене до ступеня 3", а отже, (a²)³ = (a^(2*3)) = a⁶.
Підставимо це значення в вираз:
a¹ - a' + 19 - a⁶
Це є остаточним значенням виразу.
Для спрощення виразу -23-b⁴⁰ + ((b⁵)⁴)², спростимо ((b⁵)⁴)² до b²⁰ (оскільки (b⁵)⁴ означає "b піднесене до ступеня 5, піднесене до ступеня 4"):
-23 - b⁴⁰ + b²⁰
Це є остаточним значенням виразу.
Объяснение: