Question

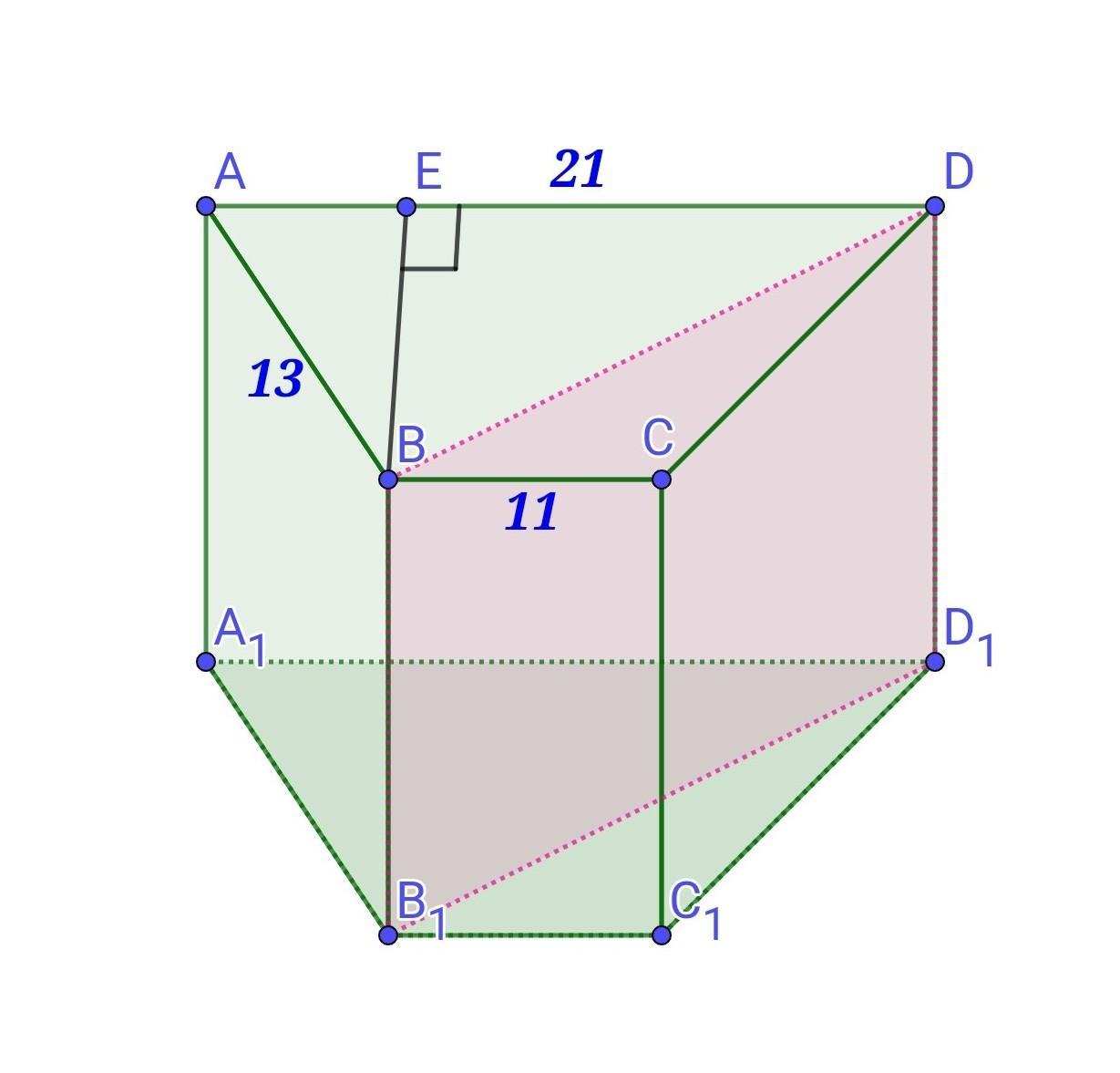
основою прямої призми ABCDA1B1C1D1 є рівнобічна трапеція ABCD основи якої BC і AD відповідно дорівнюють 11 см і 21 см, а бічна сторона- 13 см. Площа діагонального перерізу призми дорівнює 180 см2. Знайдіть площу бічної поверхні призми.

Answer 1

Ответ:

Площа бічної поверхні призми дорівнює 522 см²

Объяснение:

Основою прямої призми ABCDA1B1C1D1 є рівнобічна трапеція ABCD основи якої BC і AD відповідно дорівнюють 11 см і 21 см, а бічна сторона- 13 см. Площа діагонального перерізу призми дорівнює 180 см². Знайдіть площу бічної поверхні призми.

Нехай ABCDA₁B₁C₁D₁ - пряма призма, ABCD - ії основа, рівнобічна трапеція, ВС=11 см, AD=21 см, AB=CD=13 см. BDD₁B₁ - діагональний переріз, S(BDD₁B₁)=180см².

Знайдемо S(бічн).

S(бічн) = Р(ABCD) • h

де Р(ABCD) - периметр основи призми, h= ВВ₁ - ії висота.

1) Розглянемо рівнобічну трапецію ABCD.

BЕ⟂AD, BE - висота трапеції.

• Висота рівнобічної трапеції, яка проведена з вершини тупого кута, ділить основу трапеції на два відрізки, менший з яких дорівнює половині різниці основ, а більший — половині суми основ (середній лінії трапеції).

Отже:

$AE = \dfrac{AD - BC}{2} = \dfrac{21 - 11}{2} = \bf 5$ (см)

$ED = \dfrac{AD + BC}{2} = \dfrac{21 + 11}{2} = \bf 16$ (см)

2) Із △АЕВ (∠АЕВ=90°) за теоремою Піфагора знайдемо катет ВЕ.

$BE = \sqrt{ {AB}^{2} - {AE}^{2} } = \sqrt{ {13}^{2} - {5}^{2} } = \sqrt{169 - 25} = \bf12$ (см)

3) Із △BED (∠BED=90°) за теоремою Піфагора знайдемо гіпотенузу BD.

$BD = \sqrt{ {BE}^{2} + {ED}^{2} } = \sqrt{ {12}^{2} + {16}^{2} } = \sqrt{144 + 256} = \bf 20$ (см)

4) BDD₁B₁ - прямокутник, тому його площу знаходять за формулою:

S(BDD₁B₁) = BD • BB₁.

Отже висота призми BB₁ = S(BDD₁B₁) : BD = 180 : 20 = 9 (см).

5) Знайдемо периметр основи правильної призми:

Р(ABCD) = AB + BC + CD + AD = 13 + 11 + 13 + 21 = 58 (см).

6) Площа бічної поверхні призми:

S(бічн) = 58 • 9 = 522 (см²)

#SPJ1