Ответы
Ответ дал:
0
Ответ:
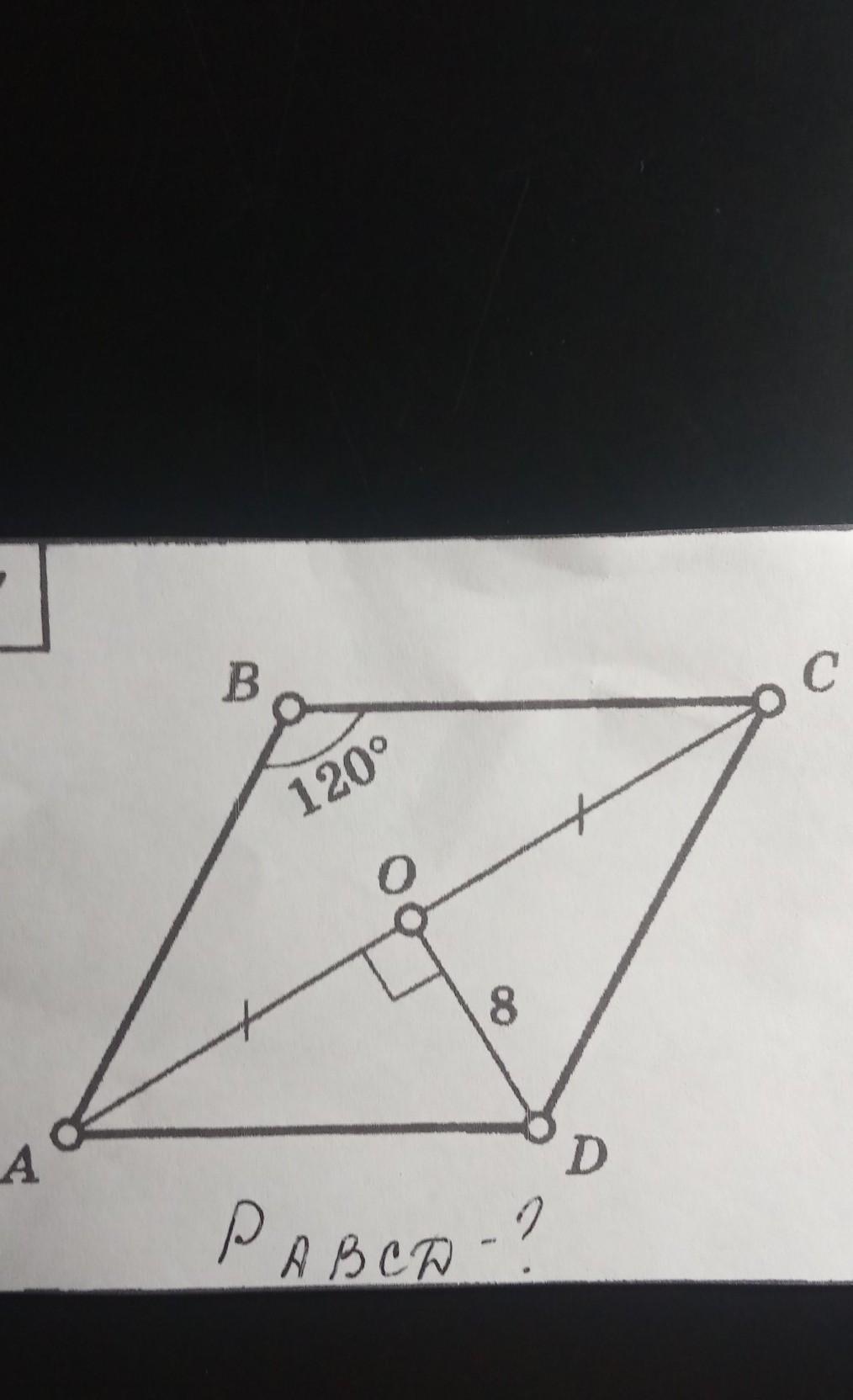
Если диагонали четырехугольника пересекаются под прямым углом и делят друг друга пополам, то этот четырехугольник – ромб. У ромба все стороны и противоположные углы равны.
∠ABC = ∠ADC
Диагонали ромба делят углы пополам.
Если достроить диагональ BD, получится треугольник BCD, рассмотрим его.
∠BDC = 120°/2 = 60°
∠CBD = 60°
Сумма внутренних углов треугольника 180°.
∠BCD + ∠BDC + ∠CBD = 180°
∠BCD + 60° + 60° = 180°
∠BCD = 180° - 60° - 60°
∠BCD = 60°
Так как у ∆BCD все углы равны, этот треугольник равносторонний. Значит у ∆BCD все стороны равны.
BD = BC = CD
Как и говорилось ранее, диагонали ромб делят друг друга пополам.
BD = 2*OD = 2*8 = 16
BC = CD = 16
P = 4*16 = 64
Ответ: P=64
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад