СПАМ-БАН!!! ДАЮ 30 БАЛІВ
Точка дотику кола, вписаного в прямокутну трапецію, ділить її більшу основу відрізки 20 см і 25 см. Знайдіть площу трапеції.
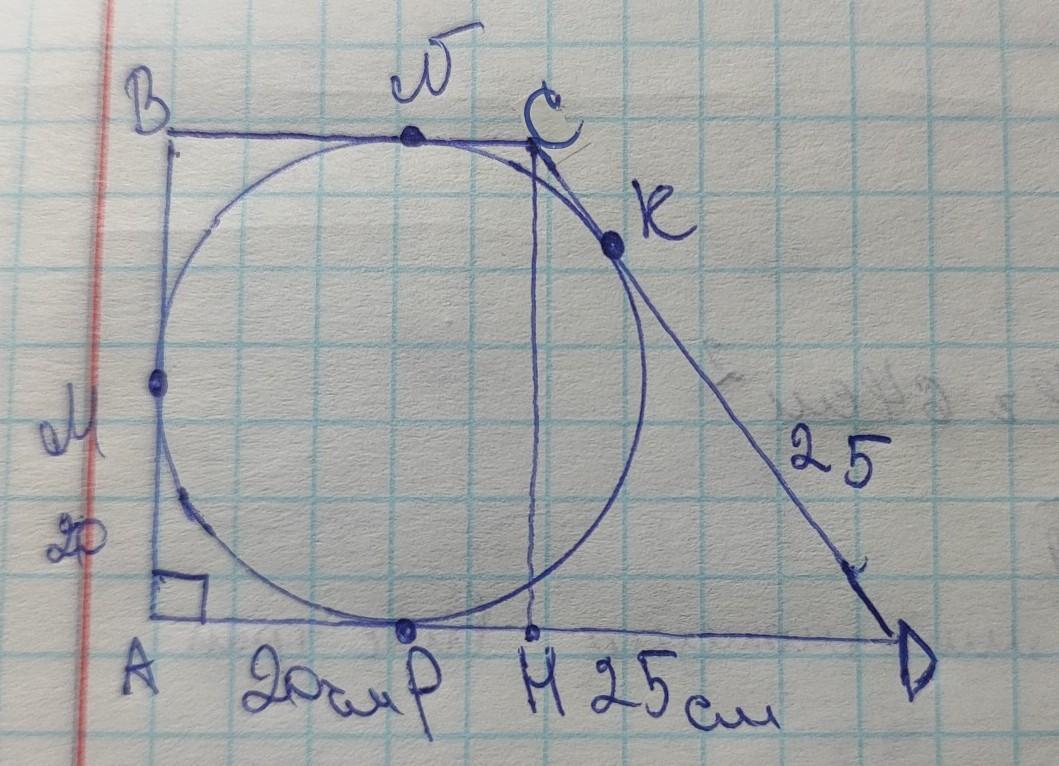
Ответы
Ответ:
Периметр трапеці: Р = 162 см
Объяснение:
Так як окружність вписана в трапецію, її діаметр дорівнює висоті трапеції, яка, в свою чергу, дорівнює АВ ( тому що кути а і в трапеції за умовою рівні 90°, і тому АВ дорівнює висоті трапеції-відстані між ВС і АD)
Проведемо діаметр трапеції через її центр паралельно АВ.
Позначимо точку дотику М (Діаметр перпендикулярний до дотичної АТ) .
А М за умовою дорівнює 20 см.
Звідси r = АМ = 20 см,
D = Н = 40 см
AB = D = 40 см.
Окружність можна вписати в чотирикутник тоді і тільки тоді, коли суми його протилежних сторін рівні.
Трапеція-чотирикутник, і тому що в неї вписана окружність,
АВ + СD=ВС + АD.
АD=20 + 25=45 см
Нехай НД =х
Тоді
СD=АD + ВС-АВ=45 + х-40=х + 5
Опустимо з вершини з перпендикуляр СН на пекло.
Отримаємо прямокутний трикутник СНД, в якому
СН=АВ = 40 см
СD=х + 5
НА=АD-ВС=45-х
Висловимо з цього трикутника СД по т. Піфагора
СD2=СН2 + НD2
(х+5)2=402+(45-х)2
2025-90х+х2 + 1600=х2+10х + 25
3600=100х
х=36
НД=36 см
АD + ВС=45 + 36=81
АВ + СD=40+(36+5)=81
Периметр трапеції
Р=81 + 81=162 см