Question

нужно доказать неравенство, помогите пожалуйста, очень срочно «Задание 1»

Answer 1

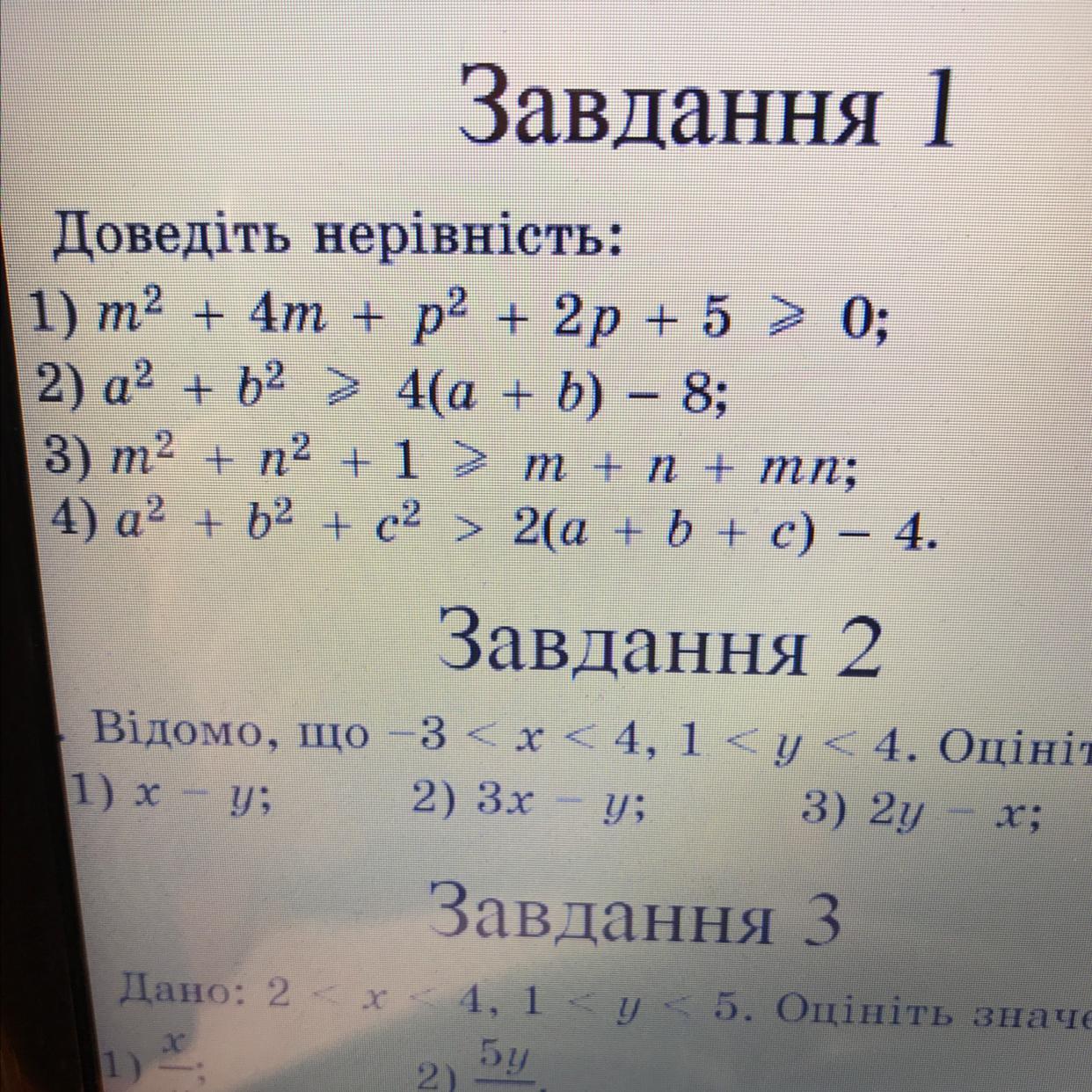
Доказать неравенство:

1) m²+4m+p²+2p+5≥0

сгруппируем

(m²+4m+4)+(p²+2p+1)=(m+2)²+(p+1)²≥0

сумма квадратов не отрицательна

2) a²+b²≥4(a+b)-8

(a²-4a+4)+b²-4b+4)=(a-2)²+(b-2)²≥0

сумма квадратов число неотрицательное

3) m²+n²+1≥m+n+mn

умножим на 2 обе части, получим

m²+n²+1 - m-n-mn≥0 | *2

2m²+2n²+2-2m-2n-2mn≥0

сгруппируем

(m²-2m+1)+(n²-2n+1)+(m²-2mn+n²)=

=(m-1)²+(n-1)²+(m-n)²≥0

сумма квадратов неотрицательна

4) a²+b²+c²>2(a+b+c)-4

(a²-2a+1)+(b²-2b+1)+(c²-2c+1)>-1

(a-1)²+(b-1)²+(c-1)²>- 1

так как сумма квадратов число неотрицательное, то она больше отрицательного числа (-1)