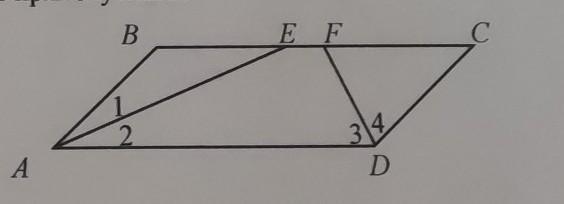
У паралелограмі ABCD: AD = 12см; кут 1 = кут 2; КУТ3 =КУТ4. Знайдіть EF, якщо AB = 3,5см. (дивіться малюнок ).
Приложения:
Ответы
Ответ дал:
0
Ответ:
EF - 5см
Объяснение:
решение находитсья на фотографии
Приложения:
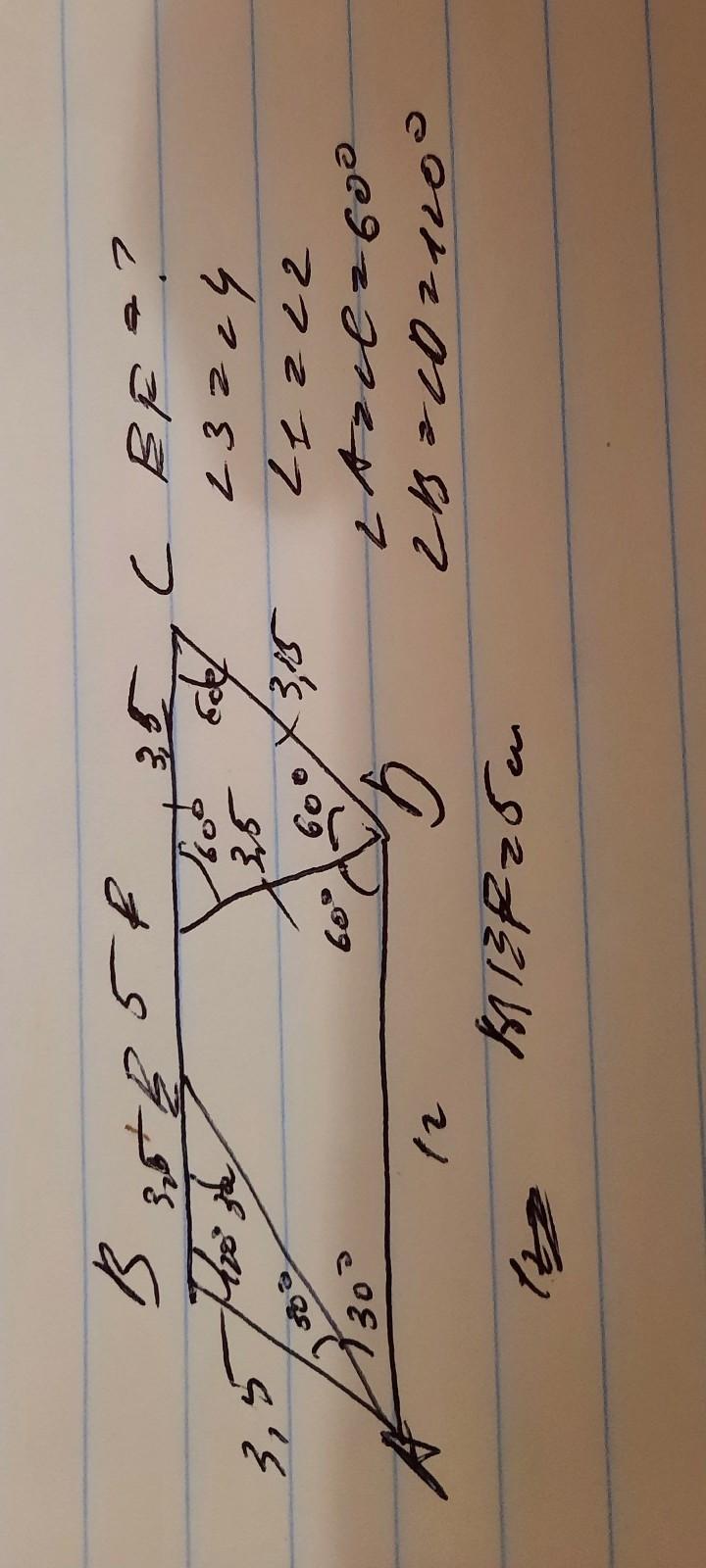
Ответ дал:
0
Відповідь:
5см
Пояснення:
Оскільки за умовою ∠1=∠2 і ∠3=∠4, то АЕ і DF є бісектрисами кутів А і D відповідно. За властивістю бісектриси кута паралелограма (бісектриса кута паралелограма відсікає ріанобедрений трикутник), трикутники АВЕ і DCF - рівнобедрені.
У трикутнику АВЕ:
АВ=ВЕ=3,5см.
У трикутнику DCF:
DC=CF; DC=AB (як протилежні сторони паралелограма);
DC=CF=3,5см.
ВС=АD (як протилежні сторони паралелограма);
ВС=АD=12см;
ВС = ВЕ + ЕF + FC;
EF = BC - BE - FC; (BE=3,5см; FC=3,5см);
ЕF = 12 - 3,5 - 3,5 = 5 (см).
Відповідь: ЕF = 5 см.
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад