Question

Помогите пожалуйста, 21 и 22 номер​

Answer 1

Ответ:

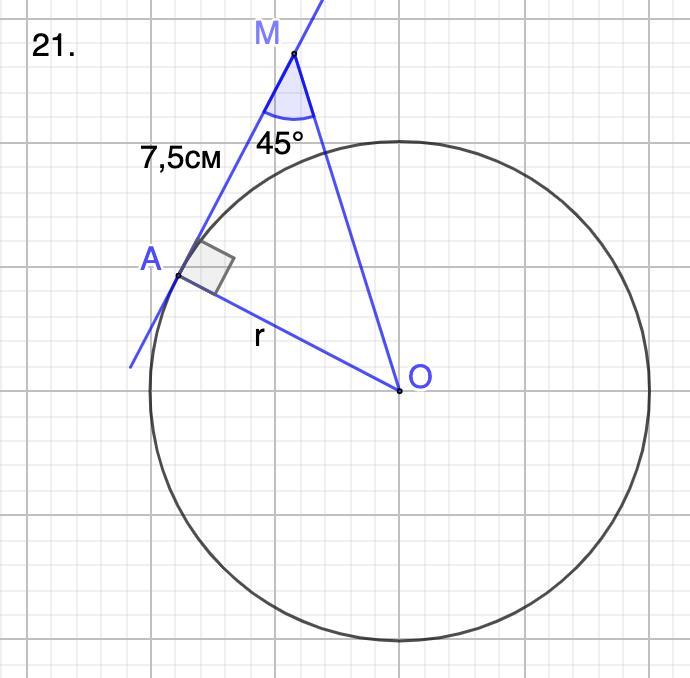
21. Радиус окружности равен 7,5 см.

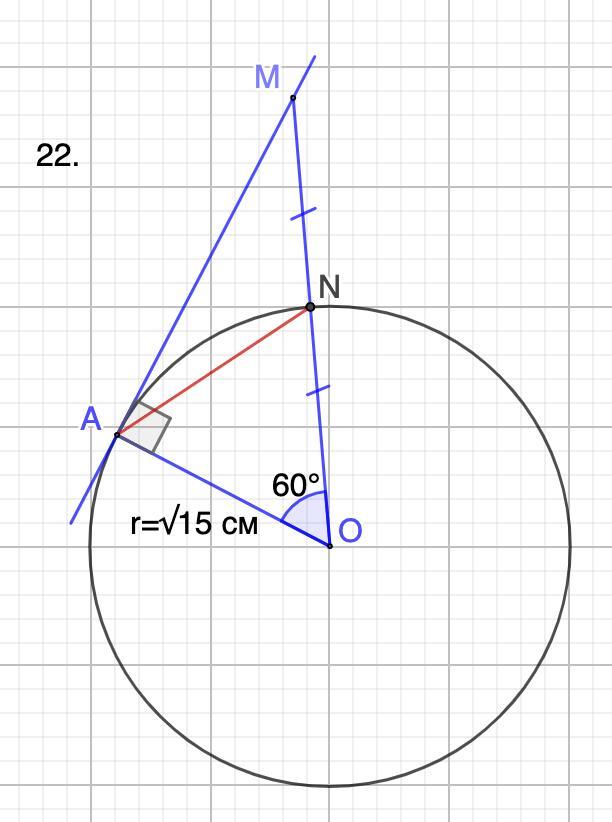
22. Отрезок AN равен √15 см.

Объяснение:

21. Дано: М ∈ Ext φ(O; r); A ∈ φ(O; r);

AM - касательная;

∠АМО = 45°; АМ = 7,5 см.

Найти: r

Решение:

Рассмотрим ΔАМО.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ∠ОАМ = 90°   ⇒   ΔАМО - прямоугольный.

∠АМО = 45° (условие)

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АОМ = 90° - ∠АМО = 90° - 45° = 45°

• Если в треугольнике есть два равных угла, то он равнобедренный.

⇒ ОА = АМ = 7,5 см

Радиус окружности равен 7,5 см.

22. Дано: М ∈ Ext φ(O; r=√15 см); A ∈ φ(O;r);

AM - касательная;

∠АМО = 60°; ОN = NM

Найти: AN

Решение:

Определим положение точки N.

Рассмотрим ΔАМО.

ОА ⊥ АМ (радиус перпендикулярен касательной)

⇒ ΔАМО - прямоугольный;

∠АМО = 90° - ∠АОМ = 90° - 60° = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ ОА = 1/2 ОМ   или ОМ = 2r

⇒ ОN = NM = r = √15 см

То есть, N ∈ φ(O;r)

Рассмотрим ΔANO;

OA = ON = r = √15 см

⇒ ΔANO - равнобедренный.

• Если в равнобедренном треугольнике есть угол 60°, то он равносторонний.

⇒ АN = r = √15 см

Отрезок AN равен √15 см.