Дана равнобедренная трапеция. Ее периметр - 28 см, и самое длинное основание - 10 см. Надо найти наикротчайшее основание, если диагональ это бисектриса широкого угла.
monertus:
Сейчас уточню.
Периметр трапеции равен 28 см, а самое длинное основание - 10 см. Вычислите кратчайшее основание трапеции, если биссектриса угла является узкой диагональю
вот прямой перевод задачи
С какого языка? Перевод не корректный. ничего не понятно.
С латышского. Могу добавить : Найдите короткое основание трапеции если диагональ - это бисектриса широкого угла.
Вот вся задача.
Решение добавлю, биссектриса острого угла, маленького угла.
Потому что при биссектрисе большого угла решения нет.
Да, спасибо!
Знаете английский?
Ответы
Ответ дал:
1
Ответ:
Меньшее основание равно 6см
Объяснение:
AD=10см
АС- биссектриса угла ∠А
Р=28см
ВС=?
Решение:
∠ВАС=∠САD, АС- биссектриса угла ∠А.
∠ВСА=∠САD, внутренние накрест лежащие при параллельных прямых ВС||АD, секущей АС
Из равенства выше указанных углов, следует равенство углов:
∠ВСА=∠ВАС, углы треугольника ∆АВС, тогда треугольник равнобедренный, углы при основании АС равны.
АВ=ВС=СD.
P=AB+BC+CD+AD; →
P=AD+3*BC; отсюда найдем ВС.
ВС=(Р-AD):3=(28-10):3=18:3=6см
_____________
P.s. — Если диагональ трапеции является биссектрисой острого угла, то меньшее основание равно боковой стороне. ВС=АВ=СD.
— Если диагональ является биссектрисой тупого угла (АС- биссектриса угла ∠С), то большее основание равно боковой стороне AD=CD=AB.
Приложения:
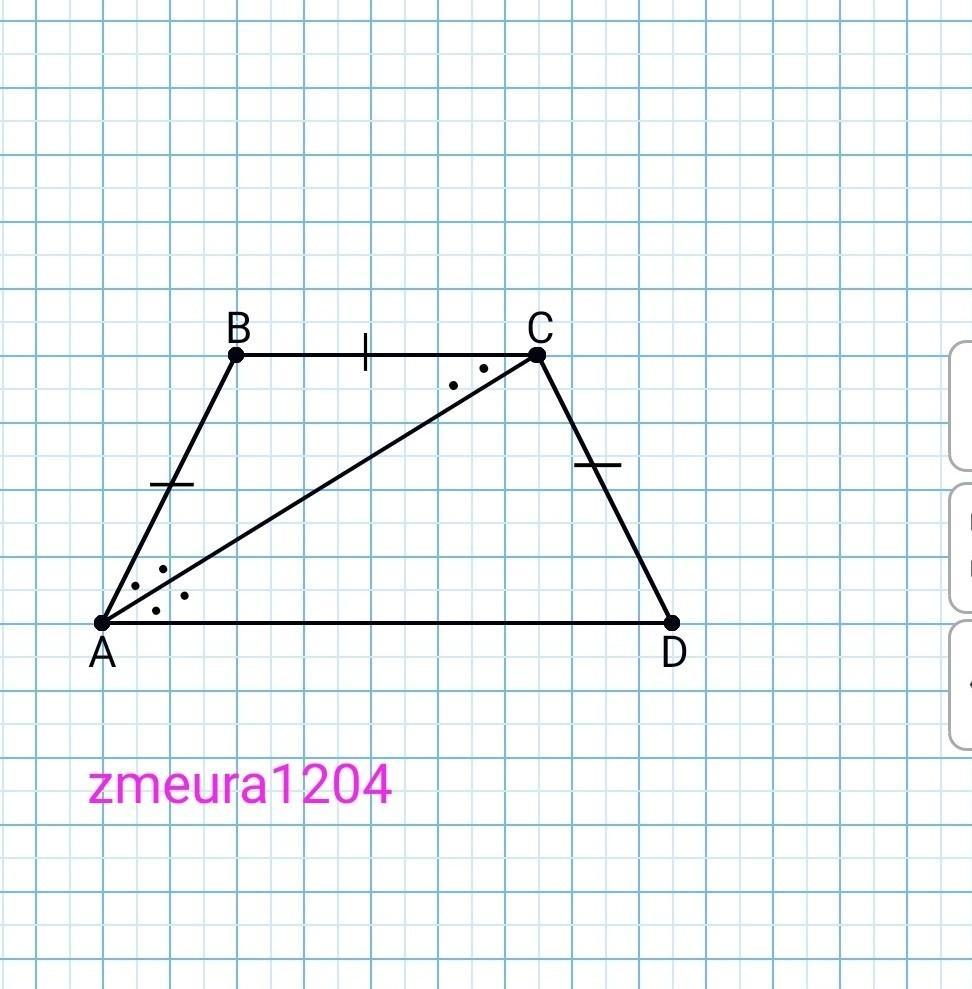
Прошу помоги мне с последним заданием
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад