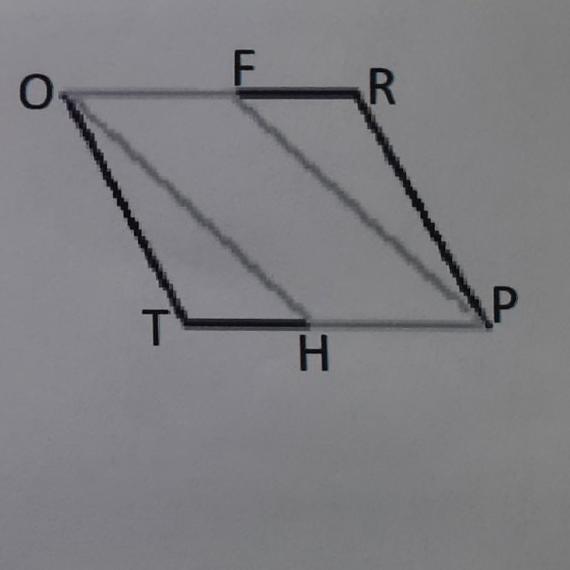
Toчки H i F -середини сторін TP і OR
паралелограма TPRO відповідно. Доведіть, що
чотирикутник OFPH - паралелограм.
Ответы
Ответ:
Для доведення, що чотирикутник OFPH - паралелограм, нам потрібно переконатися, що протилежні сторони паралельні.
Ми знаємо, що TPRO - паралелограм. Отже, сторони TP і RO - паралельні, і сторони TR і PO - також паралельні.
Також, нам сказано, що H і F - середини сторін TP і RO відповідно. Це означає, що сторона HF розташована між сторонами TP і RO і ділить їх пополам.
Таким чином, ми маємо наступне:
1. Сторони TP і RO паралельні (TPRO - паралелограм).
2. Сторони TR і PO паралельні (TPRO - паралелограм).
3. Сторона HF ділить сторони TP і RO пополам (H і F - середини сторін TP і RO).
Отже, ми бачимо, що протилежні сторони чотирикутника OFPH - паралельні (HF і OP, TP і RO), і чотирикутник OFPH відповідає визначенню паралелограма. Таким чином, чотирикутник OFPH - паралелограм.