Ответы
Ответ дал:
2
Ответ:
Вычислить значение выражения .
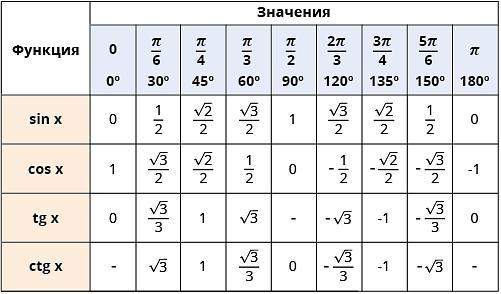
Применяем тождество : и формулы значений тригонометрических функций острых углов ( смотри вложение ) .
Приложения:
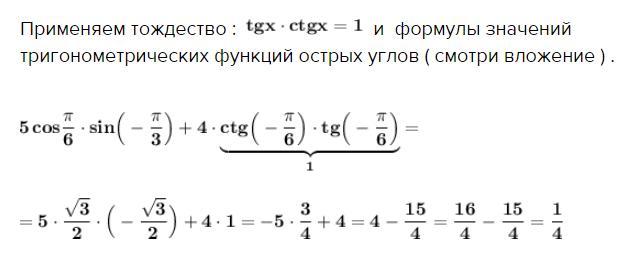
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад