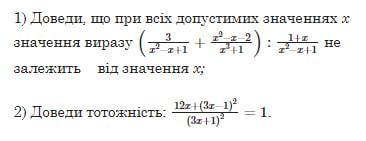Ответы
Ответ дал:
1
Ответ и Объяснение:
Информация. Формулы сокращённого умножения:
a) (a+b)² = a²+2·a·b+b²;
b) a³+b³ = (a+b)·(a²-a·b+b²);
c) (a-b)² = a²-2·a·b+b².
Решение. При упрощении выражениях применим формулы сокращённого умножения и преобразования.
1) Требуется доказать, что при всех допустимых значениях х значение выражения
не зависит от значения х.
Покажем, что результат выражения - это число, то есть результат не зависит от х.
а последнее означает при всех допустимых значениях выражение не зависит от х.
2) Требуется доказать тождество:
Покажем, что числитель выражения равен знаменателю.
12·x+(3·x-1)² = 12·x+(3·x)²-2·3·x·1+1² = 12·x+(3·x)²-6·x+1² = \\
= (3·x)²+6·x+1² = (3·x)²+2·3·x·1+1² = (3·x+1)².
Поэтому
что и требовалось доказать.
#SPJ1
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад