Ответы
Ответ дал:
3
Ответ:
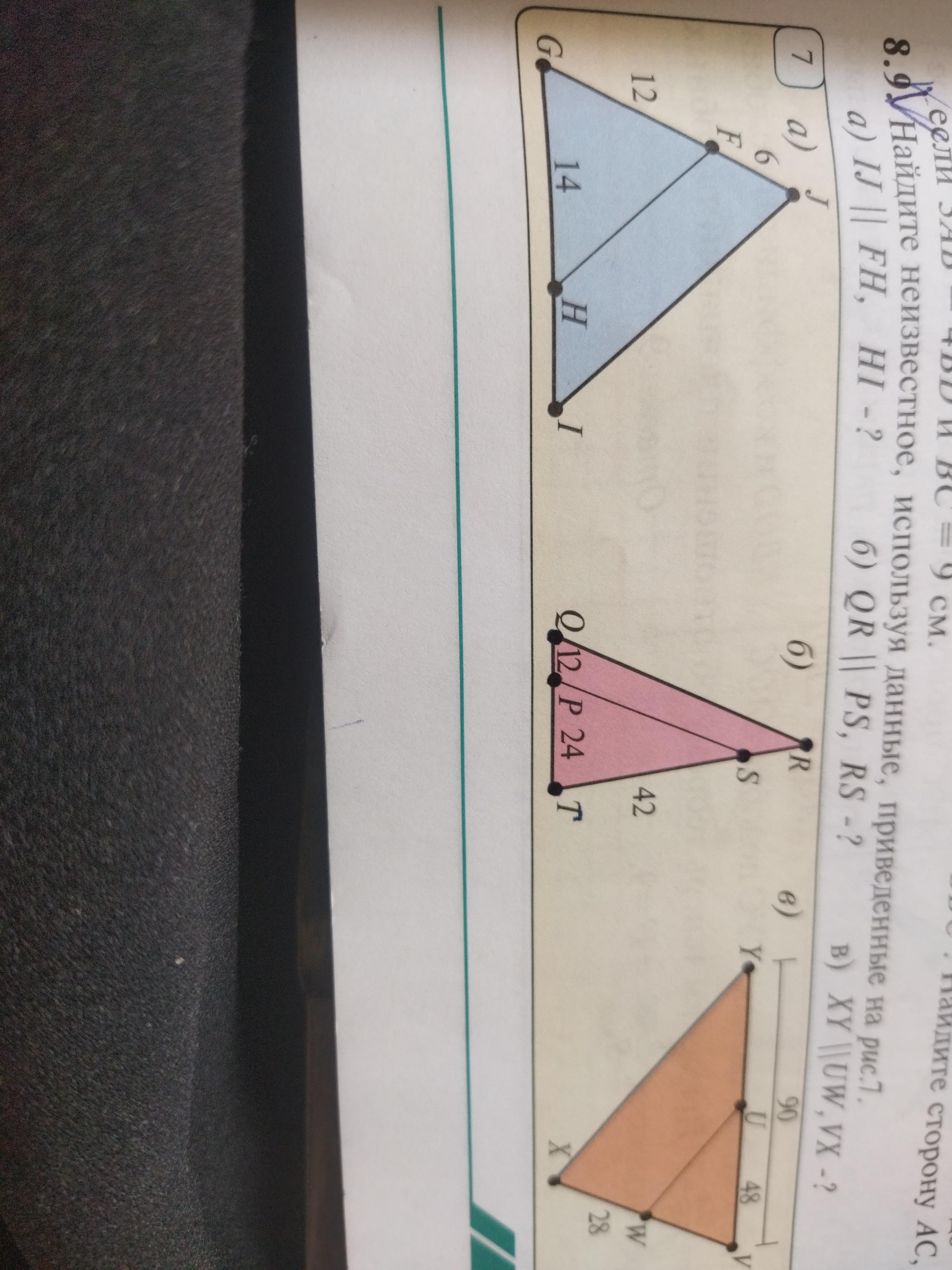
а) HI = 7 (ед)
б) RS = 21 (ед)
в) VX = 32 (ед)
Объяснение:
Теорема Фалеса обобщенная (теорема о пропорциональных отрезках):
- Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
а)
Дано: ∠JGI, IJ || FH, GF=12, FJ=6, GH=14.
Найти: HI
Согласно теореме о пропорциональных отрезках:
(ед)
б)
Дано: ∠RTQ, QR||PS, ST=42, QP=12, PT=24.
Найти: RS
Согласно теореме о пропорциональных отрезках:
(ед)
в)
Дано: ∠YVX, XY||UW, VU=48, VY=90, XW=28
Найти: VX
Согласно теореме о пропорциональных отрезках:
VX=VW+XW=VW+28.
Тогда:
90•VW=48•(VW+28)
90•VW=48•VW+1344
42•VW=1344
VW=32
Таким образом: VX = 32 + 28 = 60 (ед)
#SPJ1
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад