Question

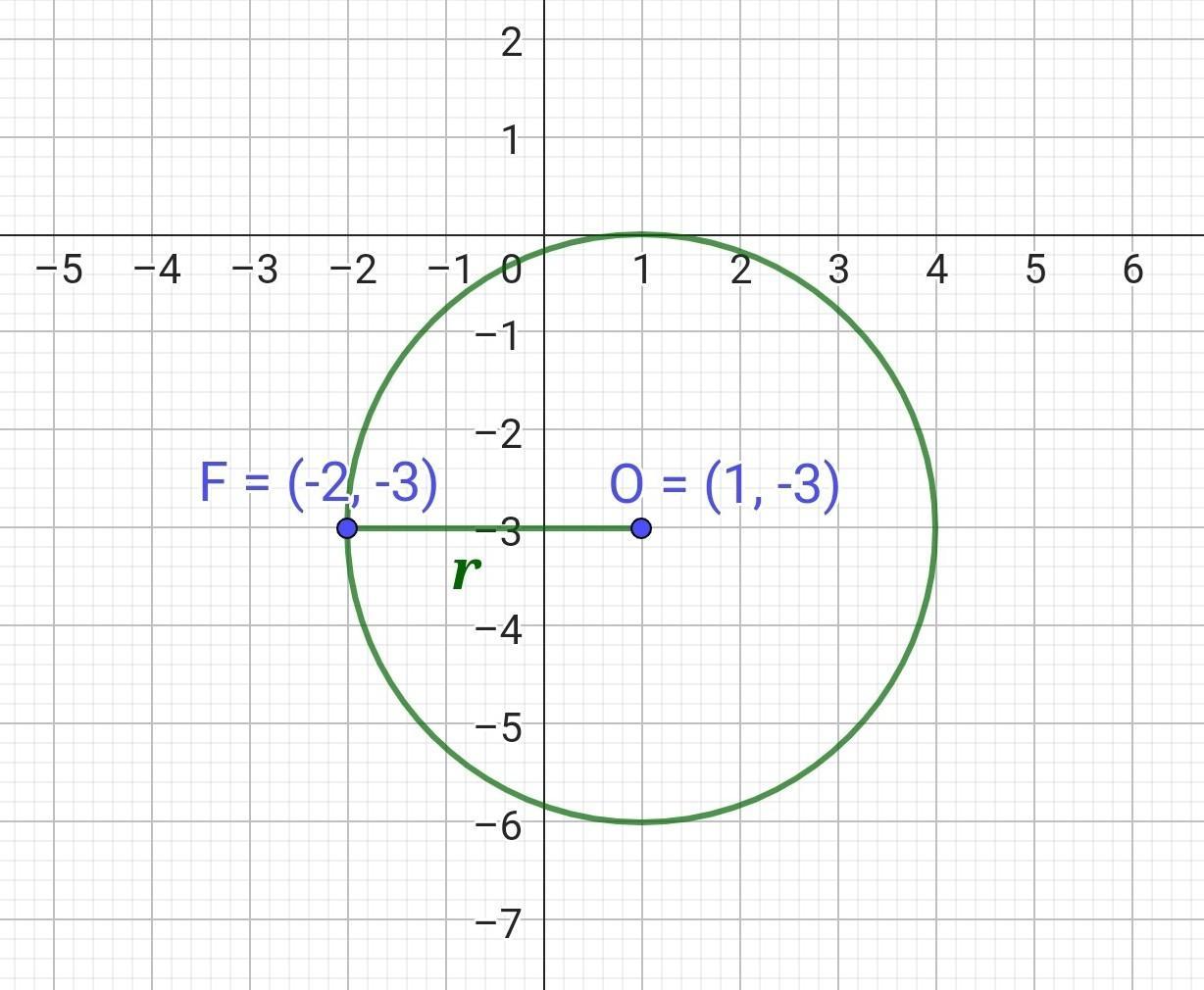
Складіть рівняння кола, яке проходить через точку F (-2; -3) і має центр у точці O (1; -3). Малюнок, умова, розв'язання з формулами, відповідь.

Answer 1

Ответ:

Рівняння кола з центром в точці О (1;-3) і радіусом 3 має вигляд: (x - 1)² + (y + 3)² = 9

Объяснение:

Складіть рівняння кола, яке проходить через точку F (-2; -3) і має центр у точці O (1; -3).

Рівняння кола з центром у точці (a;b) і радіусом r має вигляд:

(x-a)²+(y-b)²=r²

1. Знайдемо радіус кола, як відстань між точками F i O за формулою:

$\bf FO = \sqrt{ {(x_F - x_O)}^{2} + {(y_F - y_O)}^{2} }$

$FO = \sqrt{ {( - 2 - 1)}^{2} + {( - 3 - ( - 3))}^{2} } = \sqrt{ {( - 3)}^{2} + {0}^{2} } = \sqrt{9 } = \bf 3$

2. Рівняння кола з центром в точці О (1;-3) і радіусом 3 має вигляд:

(x - 1)² + (y − (-3))² = 3²;

(x - 1)² + (y + 3)² = 9

#SPJ1