сторони трикутника дорівюють 15 см, 8 см, 17 см. Визначте довжину медіани, проведеної до більшої сторони трикутника, допоможіть!!!!
Ответы
Ответ:
Довжина медіани складає 8,5 см
Пошаговое объяснение:
Сторони трикутника дорівюють 15 см, 8 см, 17 см. Визначте довжину медіани, проведеної до більшої сторони трикутника.
Нехай АВС- даний трикутник, АВ = 8 см, АС = 15 см, ВС = 17 см.
АО - медіана, АО∩ВС=О. ВО=ОС.
Знайдемо АО.
1 спосіб
Обернена теорема Піфагора:
- Якщо квадрат однієї сторони трикутника дорівнює сумі квадратів двох інших сторін, тоді трикутник є прямокутним.
Перевіримо це твердження.
АВ²+АС²=ВС²
8²+15²=17²
64+225=289
289=289
Отже, △АВС - прямокутний, з гіпотенузою ВС.
- Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи.
АО = ½ • ВС = ½ • 17 = 8,5 (см).
2 спосіб
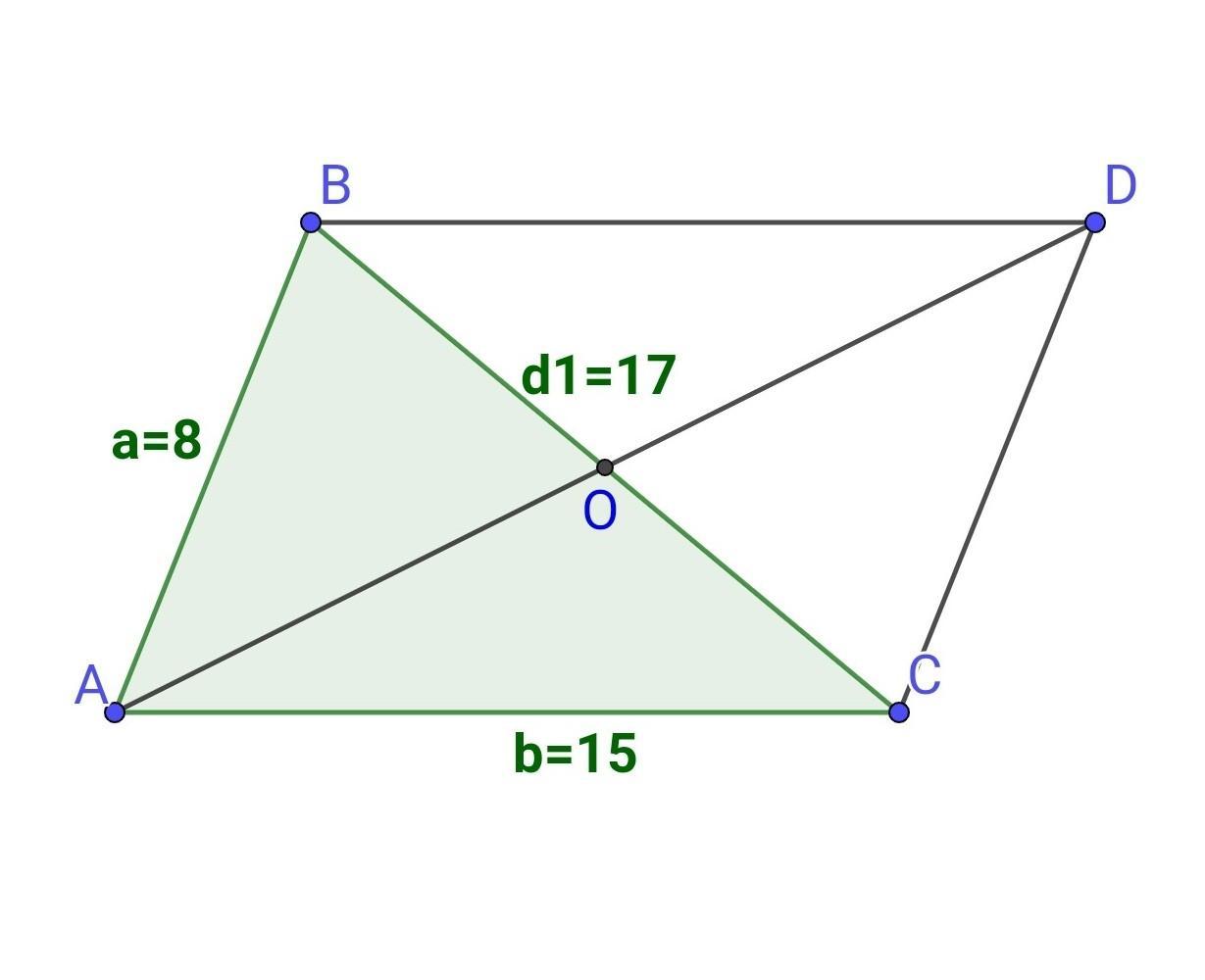
1. Продовжимо сторону △ABC і медіану АO добудувавши їх до паралелограма. В цьому випадку медіана АO △ABC буде дорівнювати половині діагоналі отриманого паралелограма, а дві сторони трикутника AB, АC - його бічним сторонам.
Сторона трикутника ВС є другою діагоналлю отриманого паралелограма.
2. Згідно з теоремою, сума квадратів діагоналей паралелограма дорівнює подвоєної сумі квадратів його сторін.
2 • (a² + b²) = d₁² + d₂²
Позначимо діагональ d₂ паралелограма як х, отримаємо:
2 • (8² + 15²) = 17² + x²
x² + 289 = 2 • (64 + 225)
x² = 2 • 289 - 289
x² = 289
x = 17
Отже, d₂ = 17
Оскільки шукана медіана дорівнює половині діагоналі паралелограма, то величина медіани трикутника складе 17 ÷ 2 = 8,5 (см)
#SPJ1