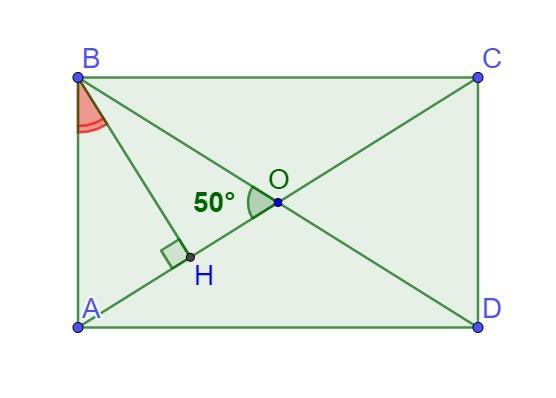
4. В прямоугольнике ABCD проведен перпендикуляр ВН к диагонали АС (рис). Найдите градусную меру угла АВН. если 2ВОА-50°.
Ответы
Ответ:
∠АВН = 25°
Объяснение:
В прямоугольнике ABCD проведен перпендикуляр ВН к диагонали АС (рис). Найдите градусную меру угла АВН, если ∠ВОА=50°.
Дано: ABCD- прямоугольник, АС и BD - диагонали, AC∩BD=O, BH⟂AC, ∠BOA=50°.
Найти: ∠ABH
РЕШЕНИЕ
1. Рассмотрим △АВО.
Так как в прямоугольнике диагонали равны и точкой пересечения делятся пополам (свойство прямоугольника), то ОВ=ОА.
Таким образом, △АВО - равнобедренный с основанием АВ (по определению).
∠ОАВ=∠ОВА - как углы при основании равнобедренного треугольника.
По теореме о сумме углов треугольника найдём эти углы:
∠ОАВ=∠ОВА=(180°-∠ВОА)÷2=(180°-50°)÷2=65°.
2. Рассмотрим прямоугольный треугольник АВН (∠АНВ=90°).
По теореме о сумме острых углов прямоугольного треугольника найдём угол АВН.
∠АВН=90°-∠НАВ=90°-∠ОАВ=90°-65°=25°.
ОТВЕТ: ∠АВН=25°.
#SPJ1