Question

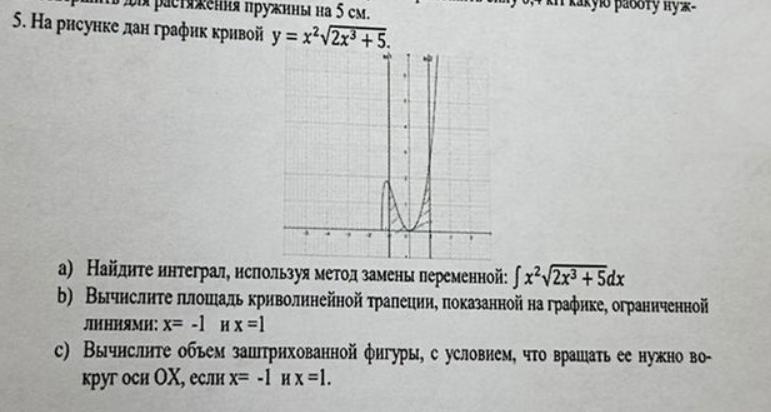
5. На рисунке дан график кривой у = x²√2x³ +5.




а) Найдите интеграл, используя метод замены переменной: ∫x²√2x³+5dx


b) Вычислите площадь криволинейной трапеции, показанной на графике, ограниченной линиями: х= -1 и х=1


с) Вычислите объем заштрихованной фигуры, с условием, что вращать ее нужно во- круг оси Ох, если х= -1 их=1

Answer 1

Ответ:

а)   $\displaystyle \int\limits x^2\sqrt{2x^3+5} \;dx=\frac{1}{9} \sqrt{(2x^3+5)^3} +C$

b)   Площадь криволинейной трапеции равна    $\displaystyle \frac{(7\sqrt{7}-3\sqrt{3}) }{9}$   ед.²

c)   Объем заштрихованной фигуры, с условием, что вращать ее нужно вокруг оси Ох, равен 2π ед.³

Объяснение:

5. На рисунке дан график кривой $\displaystyle \bf y=x^2\sqrt{2x^3+5}$.

а) Найдите интеграл, используя метод замены переменной:

$\displaystyle \bf \int\limits x^2\sqrt{2x^3+5} \;dx$

b) Вычислите площадь криволинейной трапеции, показанной на графике, ограниченной линиями: х= -1 и х=1;

с) Вычислите объем заштрихованной фигуры, с условием, что вращать ее нужно вокруг оси Оx, если х= -1 и х =1.

a) Вычислим интеграл:

$\displaystyle \int\limits x^2\sqrt{2x^3+5} \;dx$

Замена переменной:

$\displaystyle 2x^3+5 = t\\ \\ 6x^2dx=dt\\ \\x^2dx=\frac{1}{6}dt$

Получим интеграл:

$\displaystyle \frac{1}{6}\int\limits {\sqrt{t} } \, dt=\frac{1}{6}\int\limits t^{\frac{1}{2} } \;dt=\frac{1}{6}\cdot \frac{t^{\frac{3}{2} }\cdot 2}{3} =\frac{1}{9} \sqrt{t^3}+C$

Обратная замена:

$\displaystyle \int\limits x^2\sqrt{2x^3+5} \;dx=\frac{1}{9} \sqrt{(2x^3+5)^3} +C$

b) Вычислим площадь криволинейной трапеции:

         $\boxed {\displaystyle \bf S=\int\limits^b_a {(f_2(x)-f_1(x))} \, dx }$

a = -1;   b = 1;   f₁ = 0;   $f_2(x)=x^2\sqrt{2x^3+5}$

$\displaystyle S=\int\limits^1_{-1} {(x^2}\sqrt{2x^3+5} -0) \, dx =$

Данный интеграл найден в п. а)

$\displaystyle =\frac{1}{9} \sqrt{(2x^3+5)^3} \;\bigg|^1_{-1}=\frac{1}{9}(\sqrt{(2\cdot1^3+5)^3} -\sqrt{(2\cdot(-1)^3+5} )=\\\\=\frac{1}{9}(\sqrt{7^3} -\sqrt{3^3} )=\frac{(7\sqrt{7}-3\sqrt{3}) }{9}$

Площадь криволинейной трапеции равна    $\displaystyle \frac{(7\sqrt{7}-3\sqrt{3}) }{9}$   ед.²

с) Вычислим объем заштрихованной фигуры.

         $\boxed {\displaystyle \bf V=\pi \int\limits^b_a {(f_(x))^2} \, dx }$

$\displaystyle V=\pi \int\limits^1_{-1} {x^4(2x^3+5)} \, dx=\pi \int\limits^1_{-1} {(2x^7+5x^4)} \, dx =\\\\=\pi \left(\frac{2x^8}{8}+\frac{5x^5}{5}\right) \bigg|^1_{-1}=\pi \left(\frac{x^8}{4}+x^5}\right) \bigg|^1_{-1}=\\\\=\pi \left(\frac{1}{4}+1-\frac{1}{4} +1)=2\pi$

Объем заштрихованной фигуры, с условием, что вращать ее нужно вокруг оси Ох, равен 2π ед.³

#SPJ1