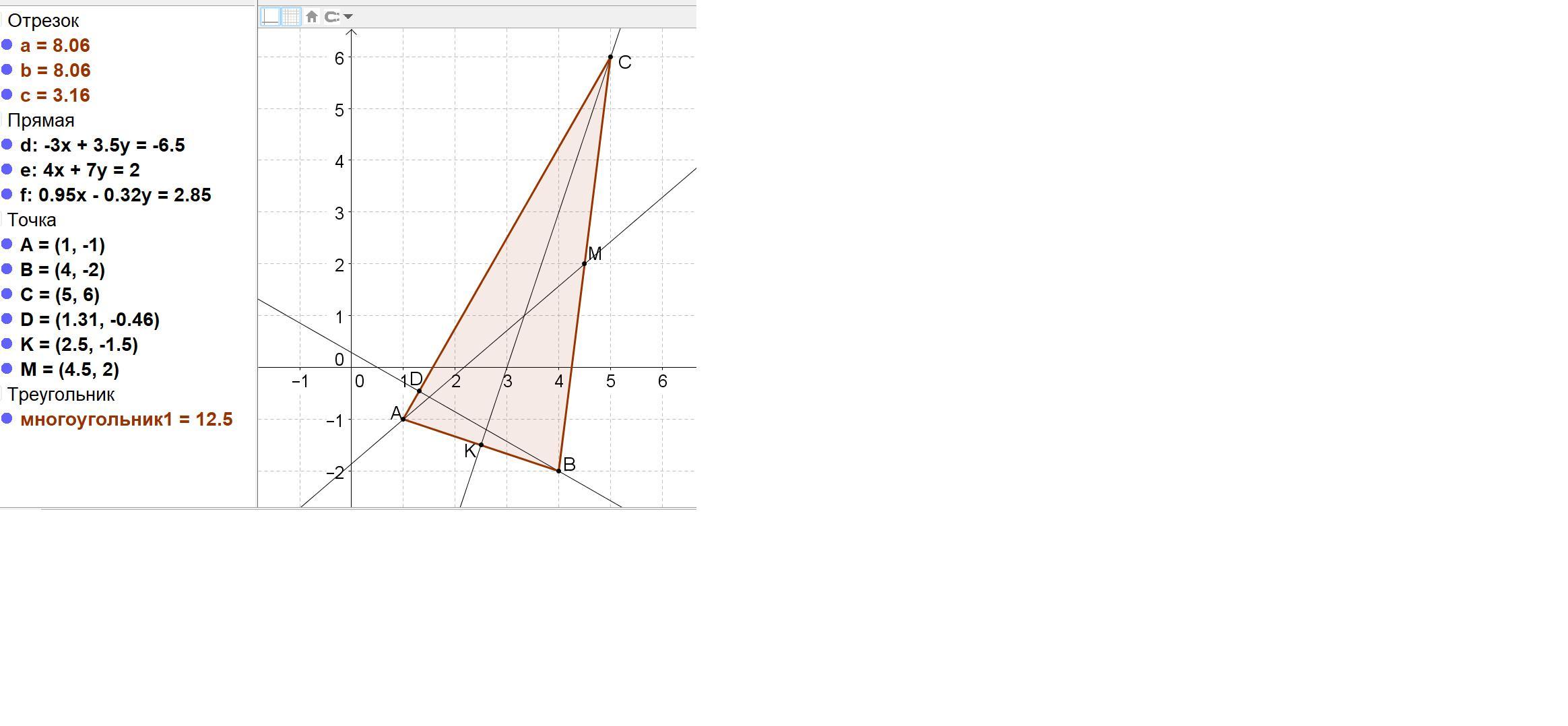
Задано вершини трикутника ABC. Знайти
рівняння медіани AM, висоти BD і
бісектриси СК.
A(1;-1), B(4;-2), C(5;6).
ТЕРМІНОВО!
Ответы
Задано вершини трикутника ABC.
Знайти рівняння медіани AM, висоти BD і бісектриси СК.
A(1;-1), B(4;-2), C(5;6).
1) Находим координаты точки M как середины стороны BС.
M = (B(4; -2) + С(5; 6))/2 = (4,5; 2).
Вектор AM = (M(4,5; 2) - A(1;-1) = (3,5; 3).
Модуль AM = √((3,5)² + 3²) = √(12,25 + 9) = √21,25 ≈ 4,6098.
Уравнение медианы AM составляем по точке A(1; -1) и направляющему вектору AM(3,5; 3).
(x – 1)/(3,5) = (y + 1)/3 каноническое.
3x – 3 = 3,5y + 3,5,
3x – 3,5y - 6,5 = 0 общее, или с целыми коэффициентами
AM: 6x – 7y - 13 = 0.
2) Находим уравнение стороны АС по точкам A(1; -1) и C(5; 6).
Вектор АС = (5-1; 6 –(-1)) = (4; 7).
Модуль (длина) равен √(4² + 7²) = √(16 + 49) =√65.
Определяем уравнение стороны АС по точке A(1;-1) и вектору АС(4; 7).
АС: (x - 1)/4 = (y + 1)/7 каноническое,
7x – 7 = 4y + 4,
7x - 4y - 11 = 0 общее.
В уравнении высоты BD как перпендикуляра к прямой AС, общее уравнение которой Ах + Ву + С = 0, коэффициенты А и В меняются на –В и А (из условия, что их скалярное произведение равно 0).
Получаем уравнение BD: 4x + 7y + C = 0. Для определения слагаемого С подставим в уравнение координаты точки B(4;-2): 4*4 + 7*(-2) + С = 0. Отсюда находим С = -16 + 14 = -2.
Тогда BD: 4x + 7y - 2 = 0.
3) Известно, что биссектриса делит угол пополам. Если на сторонах СА и СВ треугольника отложить орты (соответственно a и b) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов a и b.
Для нахождения ортов a и b необходимо знать координаты векторов СA и СВ по точкам A(1; -1), B(4; -2), C(5; 6):
СА = (-4; -7), модуль равен √65, a = ((-4/√65); (-7/√65)).
СВ = (-1; -8), модуль равен √65, b = ((-1/√65); (-8/√65)).
(a + b) = (((-4/√65) +-1/√65))/( 5√26); (-7/√65) + (-8/√65))/(5√26)) =
= ((-5√65)/(5√26)); (-15√65)/(5√26)).
По точке C(5; 6)и направляющему вектору (a + b) составляем уравнение биссектрисы CK угла C.
(x – 5)/((-5√65)/(5√26)) = (y - 6)/((-15)√65)/(5√26)).
Получилось довольно громоздкое выражение.
Можно применить другой способ, используя уравнение биссектрисы угла по уравнениям сторон угла. Вектор СВ = (-1; -8). Точка C(5; 6).
СА: 7x - 4y - 11 = 0,
СВ: (x – 5)/(-1) = (y – 6)/(-8), -8x + 40 = -y + 6
8x - y - 34 = 0.
(a1x + b1y + c1)/( √(a1² + b1²) = ± (a2x + b2y + c2)/( √(a2² + b2²)
√(7² + (-4)²) = √(49 + 16) = √65.
√(8² + (-1)²) = √(64 + 1) = √65.
Так как знаменатели равны, то приравняем числители.
7x - 4y - 11 = ±(8x - y – 34).
Получаем уравнения двух биссектрис.
7x - 4y - 11 = 8x - y – 34, x + 3y - 23 = 0 и
7x - 4y - 11 = -(8x - y – 34),
7x - 4y - 11 = -8x + y + 34,
15x - 5y - 45 = 0 или 3x - y - 9 = 0.
Осталось определить, которая из биссектрис является внутренней.
Для этого находим точку пересечения со стороной AВ, уравнение которой определяем по точкам A(1; -1) и B(4; -2).
Вектор АВ = (4-1; -2 –(-1)) = (3; -1).
АВ: (x - 1)/3 = (y + 1)/(-1) каноническое,
-x + 1 = 3y + 3,
x + 3y + 2 = 0 общее.
CK: {x + 3y - 23 = 0
AB: {x + 3y + 2 = 0. Нет решения, значит, для СК не это уравнение.
СК: { 3x - y - 9 = 0, (x3) = 9x - 3y - 27 = 0
AB: {x + 3y + 2 = 0 x + 3y + 2 = 0
10x - 25 = 0,
x = 25/10 = 2,5.
y = 3x – 9 = 3*2,5 – 9 = 7,5 – 9 = -1,5.
Уравнение СК: 3x - y - 9 = 0.