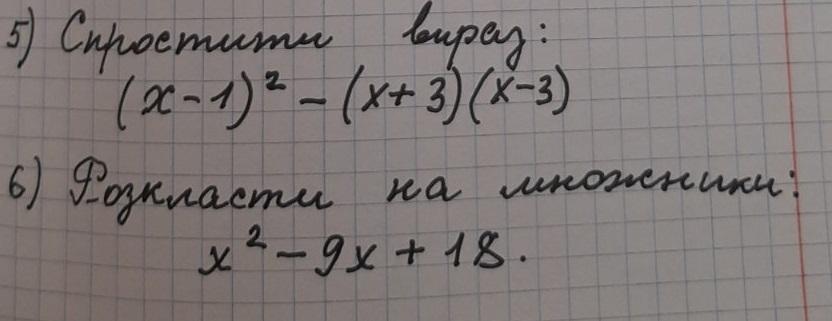Ответы
Ответ:
1)(x-1)² - (x+3)(x-3) = -2x + 10.
2)x² - 9x + 18 = (x - 3)(x - 6).
Пошаговое объяснение:
1)
Задача: Вычислить выражение (x-1)² - (x+3)(x-3).
Решение:
1. Применим свойство квадрата разности:
(x-1)² = (x-1)(x-1) = x² - 2x + 1.
2. Раскроем скобки (x+3)(x-3) с помощью правила умножения двух многочленов:
(x+3)(x-3) = x(x-3) + 3(x-3) = x² - 3x + 3x - 9 = x² - 9.
3. Теперь вычислим их разность: (x-1)² - (x+3)(x-3).
Подставим значения, которые мы получили в шагах 1 и 2:
(x-1)² - (x+3)(x-3) = (x² - 2x + 1) - (x² - 9).
4. Раскроем скобки и выполним сокращение:
(x² - 2x + 1) - (x² - 9) = x² - 2x + 1 - x² + 9.
5. Сгруппируем одночлены и выполним сложение:
(x² - 2x + 1 - x² + 9) = -2x + 10.
Таким образом, решение данной математической задачи: (x-1)² - (x+3)(x-3) = -2x + 10.
2)Для разложения квадратного трёхчлена на множители, вам нужно найти два числа, которые при перемножении дают последний коэффициент (в данном случае, 18), а при сложении дают средний коэффициент (в данном случае, -9).
Для x² - 9x + 18, мы ищем два числа, которые удовлетворяют этим условиям. Найдем такие числа:
18 может быть разложено на произведение двух чисел следующим образом:
1 * 18
2 * 9
3 * 6
Теперь мы проверим, какое из этих разложений подходит:
При сложении 1 и 18 мы получим 1 + 18 = 19, что не равно -9.
При сложении 2 и 9 мы получим 2 + 9 = 11, что также не равно -9.
При сложении 3 и 6 мы получим 3 + 6 = 9, что совпадает с -9.
Таким образом, мы можем разложить x² - 9x + 18 следующим образом:
x² - 9x + 18 = (x - 3)(x - 6).
Теперь у нас есть разложение на множители.
Ответ:
1. (x-1)2-(x+3)x(x-3) = - 2x + 10
2. x²-9x+18 = (x-3)•(x-6)
Пошаговое объяснение:
1. (x-1)2-(x+3)x(x-3) = - 2x + 10
x²-2x+1 2 - (x²-9)
x² - 2x+1-х²+9
-2x+10
2. x²-9x+18
x²-3-6+18
x•(x-3)-6(x-3)
(x-3)•(x-6)