У ромбі ABCD з вершини тупого кута в провели висоту ВР на сторону AD . Знайдіть кут PBD, якщо ZCPD = 32°, PCD = 20°.
Ответы
Ответ дал:
2
Ответ:
Для розв'язання цієї задачі важливо використовувати властивості ромба та рівнобедреного трикутника.
1. Оскільки ABCD - ромб, всі його сторони однакові за довжиною.
2. Рівні кути у ромбах ліжать проти рівних сторін. Отже, PCD = 20°.
3. Рівнобедреність трикутника BPC дає нам кут C = 20°.
4. Оскільки ромб ABCD є прямокутним, ми маємо ZCPD = 90°.
5. Тепер ми можемо знайти кут ZBPC: ZBPC = 180° - ZCPD - PCD = 180° - 32° - 20° = 128°.
6. Враховуючи кут BCP (рівний 90° - 20° = 70°), ми можемо знайти кут PBC: PBC = ZBPC - BCP = 128° - 70° = 58°.
Отже, кут PBD = 180° - PBC = 180° - 58° = 122°.
Ответ дал:
1
Ответ на фото, если что
Приложения:
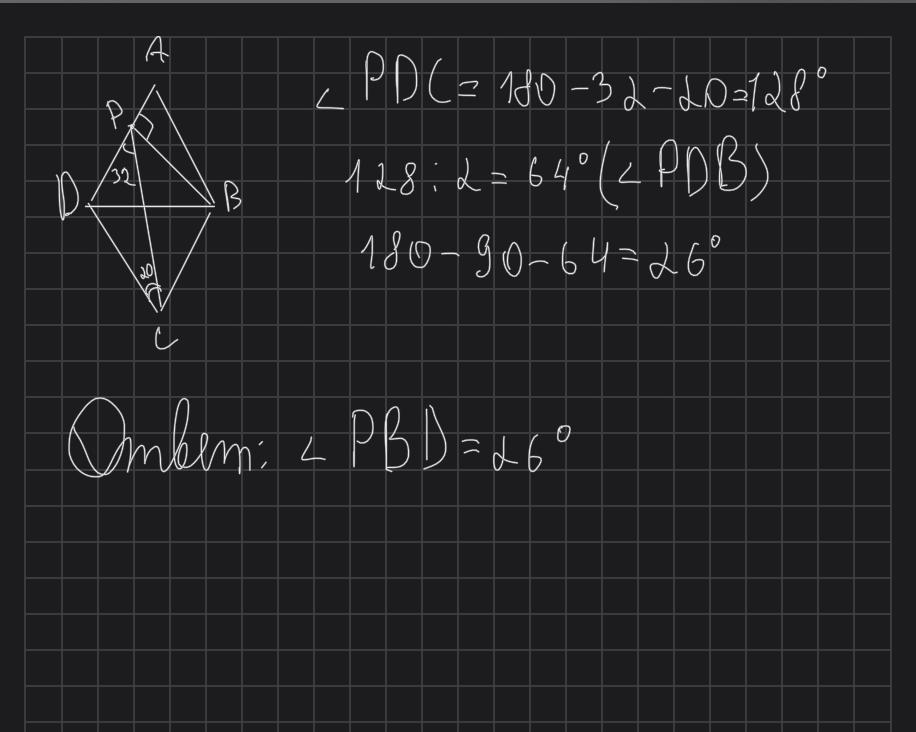
mary09pm:
спасибо
можете отметить как лучший ответ?)
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад