Question

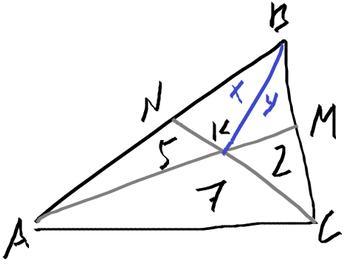
На сторонах ВC и AB ∆ ABC выбраны соответственно точки M и N. Прямые АМ и CN пересекаются в точке к . Площади треугольников ANK, АКС и КМС равны 5, 7 и 2 соответственно. Найти площадь четырехугольника NBMK.​

Answer 1

Ответ:

70/13

Объяснение:

NBK=x ; MBK=y

Площади треугольников с равными высотами относятся как основания.

Треугольники NBK и KBC имеют общую высоту из вершины B - их площади относятся как основания, NK/KC.

Треугольники NAK и KAC имеют общую высоту из вершины A - их площади относятся как основания, NK/KC.

NBK/KBC =NK/KC =NAK/KAC =5/7

x/(y+2)=5/7

Аналогично

ABK/KBM =AK/KM =ACK/KCM =7/2

(x+5)/y=7/2

x=40/13 ; y=30/13