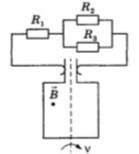
.Хорошо проводящая рамка площадью 30 см^2 вращается в однородном магнитном поле с индукцией 2 Тл перпендикулярно оси вращения рамки с частотой 50 Гц (рис). Скользящие контакты от рамки подключены к цепи, состоящей из резисторов с сопротивлением: R1 = 6 Ом, R2 = 3 Ом, R3 = 9 Ом. Найдите максимальный ток, протекающий через резистор R3 во время вращения рамки.
Ответы
Ответ:
Для решения данной задачи воспользуемся законом электромагнитной индукции Фарадея:
$$\mathcal{E} = -N \frac{d\Phi}{dt},$$
где $\mathcal{E}$ - ЭДС, индуцированная в рамке, $N$ - количество витков, $\Phi$ - поток магнитной индукции через рамку.
Поток магнитной индукции можно выразить через индукцию магнитного поля:
$$\Phi = BScos\alpha,$$
где $B$ - индукция магнитного поля, $S$ - площадь рамки, $\alpha$ - угол между нормалью к рамке и вектором магнитной индукции.
При вращении рамки в однородном магнитном поле поток магнитной индукции меняется от максимального значения ($\alpha = 0$) до минимального ($\alpha = \pi$). В этом случае ЭДС в рамке будет меняться от максимального значения до минимального с удвоенной частотой:
$$\mathcal{E}_{max} = NBS, \quad \mathcal{E}_{min} = -NBS.$$
Тогда максимальная мощность, вырабатываемая в рамке:
$$P_{max} = \frac{(\mathcal{E}_{max})^2}{R_1+R_2+R_3}.$$
Во время вращения рамки эта мощность будет выделяться на резисторах, поэтому максимальный ток через резистор $R_3$ будет равен:
$$I_{max} = \sqrt{\frac{P_{max}}{R_3}}.$$
Подставляя значения, получаем:
$$I_{max} = \sqrt{\frac{(NBS)^2}{(R_1 + R_2 + R_3)R_3}}} = \sqrt{\frac{(30 \cdot 2)^2}{(6 + 3 + 9) \cdot 9}}} \approx 1,8 \ \text{A}.$$