Question

1. Решите задачу с помощью системы уравнений. Расстояние между городами А и В составляет 120 км. Катер проходит этот путь по течению реки за 3 часа, против течения за 4 часа. Найдите скорость катера в стоячей воде и скорость течения реки.

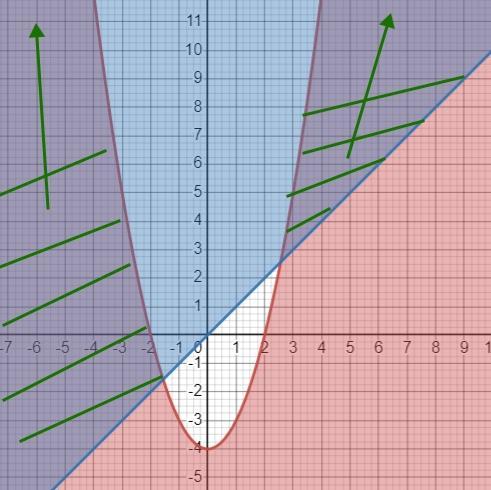
2. Найдите множество точек координатной плоскости, которое задано системой неравенств: у≤х²-4
у≥х​

Answer 1

Ответ:

1. скорость катера равна 35 км/час,

скорость течения равна  5 км/час.

2. на рисунке

Объяснение:

1.

Пусть скорость катера х км/час

скорость течения у км/час

Составим и решим систему уравнений

$\displaystyle \left \{ {{4(x-y)=120} \atop {3(x+y)=120}} \right. \left \{ {{x-y=30} \atop {x+y=40 }} \right. \left \{ {{x=30+y \hfill} \atop {30+y+y=40}} \right. \left \{ {{x=35} \atop {y=5}} \right.$

Таким образом, скорость катера 35 км/час, скорость течения 5 км/час.

2.

Строим график  у = х²- 4. Это парабола.

Для этого берем известный  график у = х² и смещаем его на 4 единицы вниз по оси OY.

Определяем, где выполняется неравенство  у ≤ х²- 4. Для этого берем любую точку, подставляем в неравенство и таким образом определяем, выполняется ли оно на области, которой принадлежит точка.

Неравенство выполняется снаружи параболы.

Строим график у = х (это прямая)  и, аналогично первой функции,  определяем, где выполняется неравенство  у ≥ х​.

Оно выполняется выше графика у = х.

Пересечение этих областей и есть искомое множество точек.