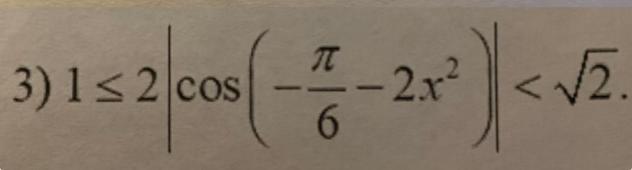Question

Помогите решить неравенство

Answer 1

Ответ:

3) Решить тригонометрическое неравенство .

   $\bf \displaystyle 1\leq 2\cdot \Big|\ cos\Big(-\frac{\pi }{6}-2x^2\Big)\Big| < \sqrt2\ \ \Rightarrow \ \ \ \ \frac{1}{2}\leq \Big|\ cos\Big(\frac{\pi }{6}+2x^2\Big)\Big| < \frac{\sqrt2}{2}\ \ ,$  

Сделаем замену :  $\bf t=\dfrac{\pi }{6}+2x^2$

Воспользовались чётностью функции косинус :  $\bf cos(-t)=cos\, t$  .

Теперь перепишем неравенство через переменную  t .

  $\bf \displaystyle \frac{1}{2}\leq |\ cos\, t\ | < \frac{\sqrt2}{2}$  

Это неравенство равносильно системе :

  $\left\{\begin{array}{l}\bf \, |\cos\, t\ | < \dfrac{\sqrt2}{2}\\\bf |\ cost\ |\geq \dfrac{1}{2}\end{array}\right$  

Решаем каждое неравенство по отдельности .

$\bf \displaystyle a)\ \ |\, cos\, t\ | < \frac{\sqrt2}{2}\ \ \ \Longleftrightarrow \ \ \ -\frac{\sqrt2}{2} < cos\, t < \frac{\sqrt2}{2}\\\\\\\frac{\pi }{4}+\pi n < t < \frac{3\pi }{4}+\pi n\ \ ,\ \ n\in Z\\\\\\t\in \Big(\ \frac{\pi }{4}+\pi n\ ;\ \frac{3\pi }{4}+\pi n\ \Big)\ ,\ \ n\in Z$  

На рисунке 3а) отмечены интервалы, на которых верно неравенство а)

$\bf \displaystyle b)\ \ |\ cost\ |\geq \frac{1}{2}\ \ \ \Longleftrightarrow \ \ \ \left[\begin{array}{l}\bf cost\geq \dfrac{1}{2}\\\bf cost\leq -\dfrac{1}{2}\end{array}\right$    

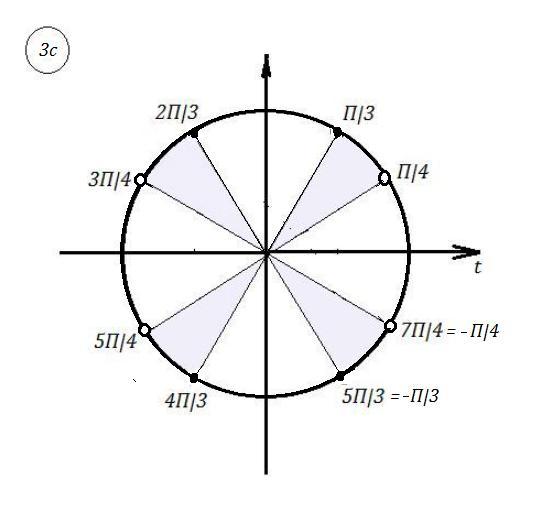
Решаем совокупность неравенств и отмечаем на тригонометрическом круге нужные промежутке . Смотри рис. 3б) .

$\displaystyle \bf cost\geq \frac{1}{2}\ \ \Rightarrow \ \ \ -\frac{\pi }{3}+2\pi k\leq \ t\ \leq \frac{\pi }{3}+2\pi k\ \ ,\ k\in Z\\\\\\cost\leq -\frac{1}{2}\ \ \Rightarrow \ \ \ \frac{2\pi }{3}+2\pi k\leq \ t\ \leq \frac{4\pi }{3}+2\pi k\ \ ,\ k\in Z$  

Можно записать так :

$\bf \displaystyle t\in \Big[\ -\frac{\pi }{3}+2\pi k\ ;\ \frac{\pi }{3}+2\pi k\ \Big]\cup \Big[\ \frac{2\pi }{3}+2\pi k\ ;\ \frac{4\pi }{3}+2\pi k\ \Big]\ ,\ k\in Z$  

Объединение этих множеств можно записать короче , но уже с периодом Пk :   $\bf \displaystyle t\in \Big[-\frac{\pi }{3}+\pi k\ ;\ \frac{\pi }{3}+\pi k\ \Big]$  ,  потому что  

 $\displaystyle \bf \frac{2\pi }{3}=-\frac{\pi }{3}+\pi\ \ ,\ \ \frac{4\pi}{3}=\frac{\pi }{3}+\pi$   .

c)  Окончательно надо записать пересечение множеств из  а)  и  b) .

$\bf \displaystyle \left\{\begin{array}{l}\bf t\in \Big(\ \dfrac{\pi}{4}+\pi n\ ;\ \dfrac{3\pi}{4}+\pi n\ \Big)\ ,\ n\in Z\\\bf \ t\in \Big[\, -\dfrac{\pi}{3}+\pi k\ ;\ \dfrac{\pi}{3}+\pi k\ \Big]\ ,\ k\in Z\end{array}\right\ \ \ \ \Rightarrow$    

  $\bf \displaystyle t\in \Big[\ \frac{2\pi}{3}+\pi m\ ;\, \frac{3\pi}{4}+\pi m\ \Big)\cup \Big(\ \frac{\pi }{4}+\pi m\ ;\ \frac{\pi }{3}+\pi m\ \Big]\ ,\ \ m\in Z$  

Заменим теперь переменную  t  на выше указанное выражение и решим два неравенства .

$\bf \displaystyle \frac{2\pi}{3}+\pi m\ \leq \frac{\pi }{6}+2x^2\ < \frac{3\pi}{4}+\pi m\ \ \ \ ili\ \ \ \ \frac{\pi }{4}+\pi m\ < \dfrac{\pi}{6}+2x^2\leq \frac{\pi }{3}+\pi m\ ,\ m\in Z\\\\\\\frac{\pi}{2}+\pi m\ \leq 2x^2\ < \frac{7\pi}{12}+\pi m\ \ \ \ ili\ \ \ \ \frac{\pi }{12}+\pi m\ < 2x^2\leq \frac{\pi }{6}+\pi m\ \ ,\ \ m\in Z$

$\bf \displaystyle \frac{\pi}{4}+\dfrac{\pi m}{2}\ \leq x^2\ < \frac{7\pi}{24}+\dfrac{\pi m}{2}\ \ \ \ ili\ \ \ \ \frac{\pi }{24}+\dfrac{\pi m}{2}\ < x^2\leq \frac{\pi }{12}+\frac{\pi m}{2}\ \ ,\ \ m\in Z$      

Окончательно будем иметь :  

$\bf \displaystyle x^2\in \Big[\, \frac{\pi}{4}+\dfrac{\pi m}{2}\ ;\ \frac{7\pi}{24}+\dfrac{\pi m}{2}\ \Big)\ \cup \ \Big(\ \frac{\pi }{24}+\dfrac{\pi m}{2}\ ;\ \frac{\pi }{12}+\dfrac{\pi m}{2}\ \Big]\ \ ,\ \ m\in Z$        

$\bf \displaystyle x^2\in \Big[\, \frac{\pi}{4}\, (1+2m)\ ;\ \frac{\pi}{24}\, (7+12m)\ \Big)\ \cup \ \Big(\ \frac{\pi }{24}\, (1+12m)\ ;\ \frac{\pi }{12}\, (1+6m)\ \Big]\ \ ,\ \ m\in Z$

$\displaystyle \bf x\in \Big(\, -\sqrt{\frac{\pi}{24}\, (7+12m)}\ ;\ -\sqrt{\frac{\pi}{4}\, (1+2m)}\ \Big]\ \cup \ \Big[\ \sqrt{\frac{\pi }{4}\, (1+2m)}\ ;\ \sqrt{\frac{\pi }{24}\, (7+12m)}\ \Big)\cup \\\\\\\cup \ \Big[ -\sqrt{\frac{\pi}{12}\, (1+6m)}\ ;\ -\sqrt{\frac{\pi}{24}\, (1+12m)}\ \Big)\ \cup \ \Big(\ \sqrt{\frac{\pi }{24}\, (1+12m)}\ ;\ \sqrt{\frac{\pi }{12}\, (1+6m)}\ \Big]$