Помогите решить неравенство
Приложения:
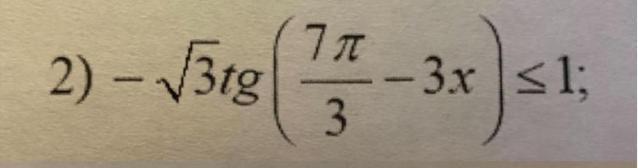
Аноним:
видите да модератор какой. ни тригонометрию не знает ничего
Ответы
Ответ дал:
3
Ответ:
Решить тригонометрическое неравенство .
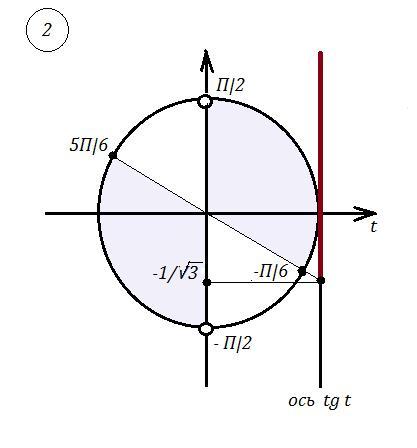
Сделаем замену : .
На оси тангенсов отмечаем значение функции tg t = - 1/√3 и определяем , где лежат значения функции , бОльшие -1/√3 . Надо не забыть выколоть точки , в которых не существует функция tg t , то есть точки t = П/2+Пn , n∈Z .
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад