Question

срочн помогите
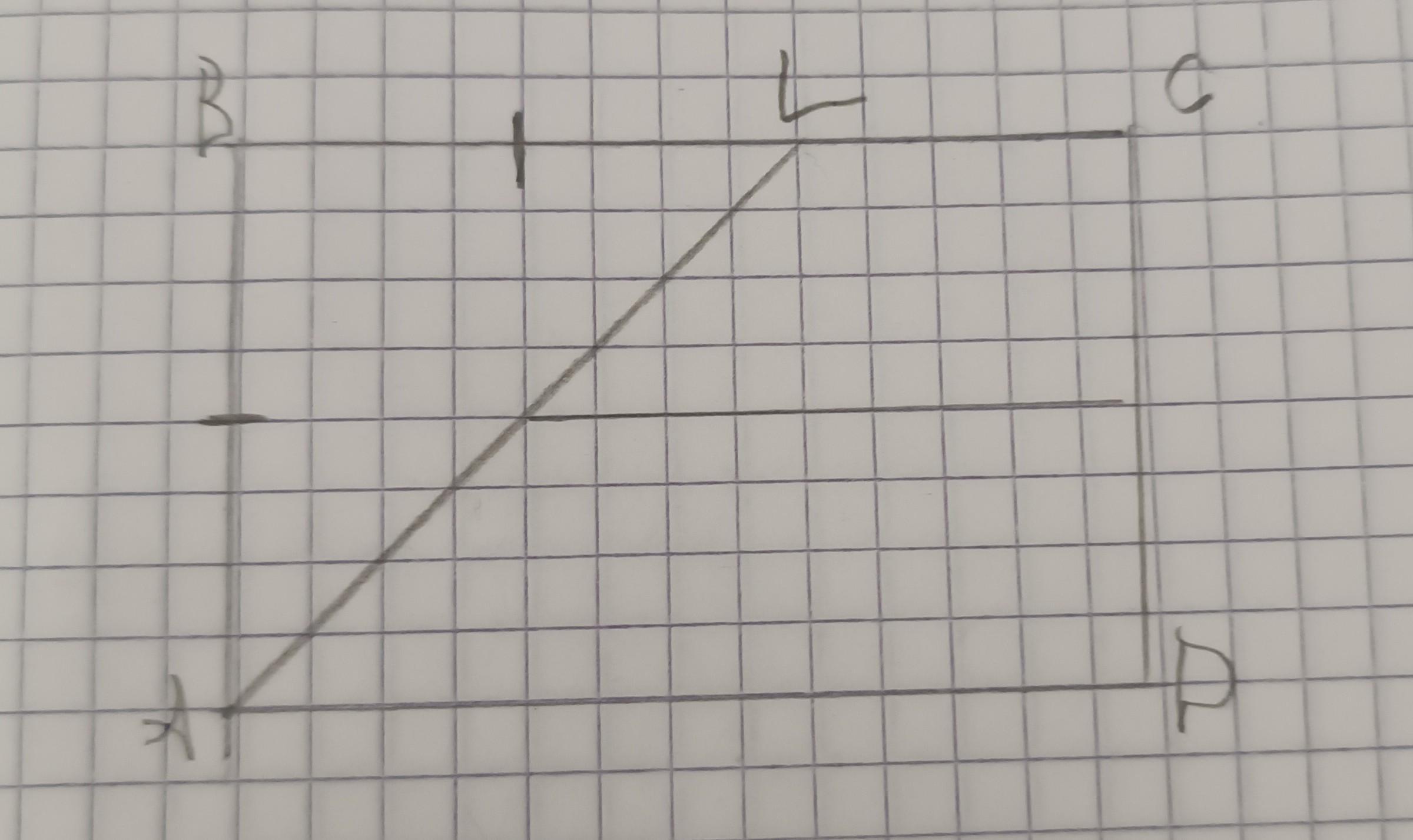
Дано: ABCD - прямоугольник
AL - биссектриса угол A
BL= 6см, LC = 3см
Найти: P ABCD, MN - средняя линия
​

Answer 1

Ответ:

Для нахождения площади прямоугольника ABCD, вы можете воспользоваться формулой для площади прямоугольника:

P_ABCD = AB * BC

Известно, что прямоугольник ABCD имеет биссектрису угла A (AL), и длины отрезков BL и LC. Поэтому мы можем выразить длину стороны AB следующим образом:

AB = 2 * BL + LC

AB = 2 * 6см + 3см = 12см + 3см = 15см

Теперь мы знаем длины сторон AB и BC, и можем найти площадь прямоугольника:

P_ABCD = AB * BC = 15см * 6см = 90 квадратных см.

Чтобы найти среднюю линию MN прямоугольника ABCD, вы можете воспользоваться следующей формулой:

MN = 0.5 * BD,

где BD - длина диагонали прямоугольника.

Для нахождения длины BD, можно воспользоваться теоремой Пифагора в треугольнике ABC:

BD² = AB² + AC²,

где AB = 15см (как мы уже вычислили), а AC = LC = 3см.

BD² = 15см² + 3см² = 225см² + 9см² = 234см².

Теперь найдем длину BD:

BD = √234 см ≈ 15,30 см

Теперь найдем среднюю линию MN:

MN = 0.5 * BD = 0.5 * 15,30 см ≈ 7,65 см.

Следовательно, длина средней линии MN прямоугольника ABCD равна примерно 7,65 см.