Спростіть вираз:
1) (y + 3)/(2y + 2) - (y + 1)/(2y - 2) + 3/(y ^ 2 - 1) 2) (2b ^ 2 - b)/(b ^ 3 + 1) - (b - 1)/(b ^ 2 - b + 1)
ПОМОГИ СРОЧНО ДАЮ 20 БАЛЛОВ!!!!
Приложения:
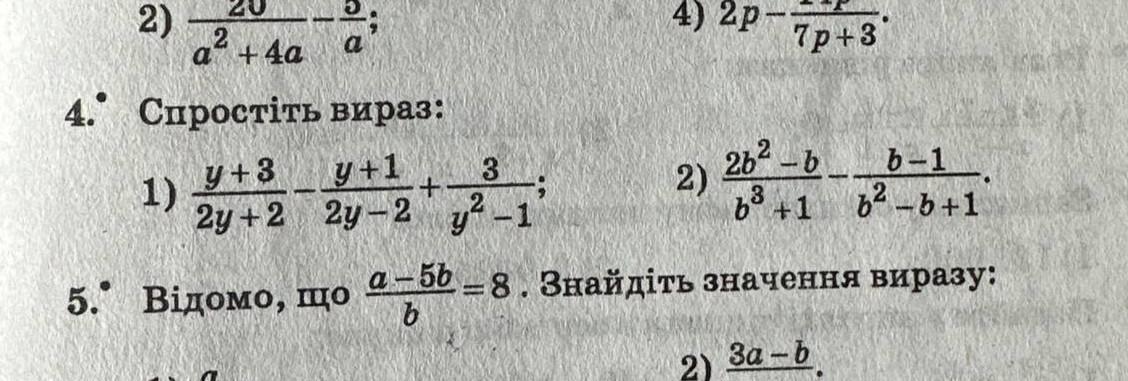
Ответы
Ответ дал:
0
Ответ:
Мозгокошка:
Здравствуйте!Очень нужна Ваша помощь с геометрией.Пожалуйста,если Вы не заняты и у Вас есть возможность,помогите.Была бы безумно благодарна.В любом случае спасибо и хорошего Вам дня
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад