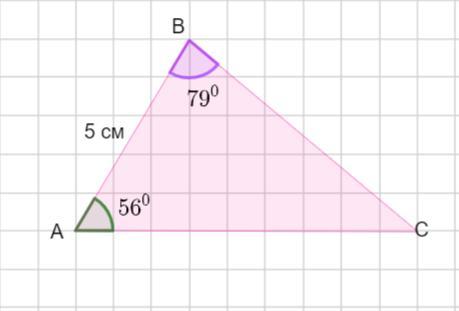
Сторона трикутника дорівнює 5 см а прилеглі до неї кути дорівнюють 79 градусів і 56 градусів. Знайдіть радіус кола описаного навколо цього трикутника.
Будь ласка терміновоооо даю 35 балів
Ответы
Ответ дал:
3
Ответ:
см
Объяснение:
Сторона треугольника равна 5 см, а прилещажие к ней углы равны 79 градусов и 56 градусов . Найти радиус описанной около треугольника окружности.
Пусть дан ΔАВС , АВ =5 см, ∠А =56°, ∠В =79°.
Сумма углов треугольника равна 180°. Найдем градусную меру ∠С
∠С =180° - ( 79° +56°) =180° - 135° = 45°.
Радиус окружности, описанной около треугольника, определяется по формуле:
где α - угол, противолежащий стороне а.
Значит,
см
Значит, радиус окружности, описанной около треугольника равен
см
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад