Ответы
Ответ дал:
1
Відповідь:
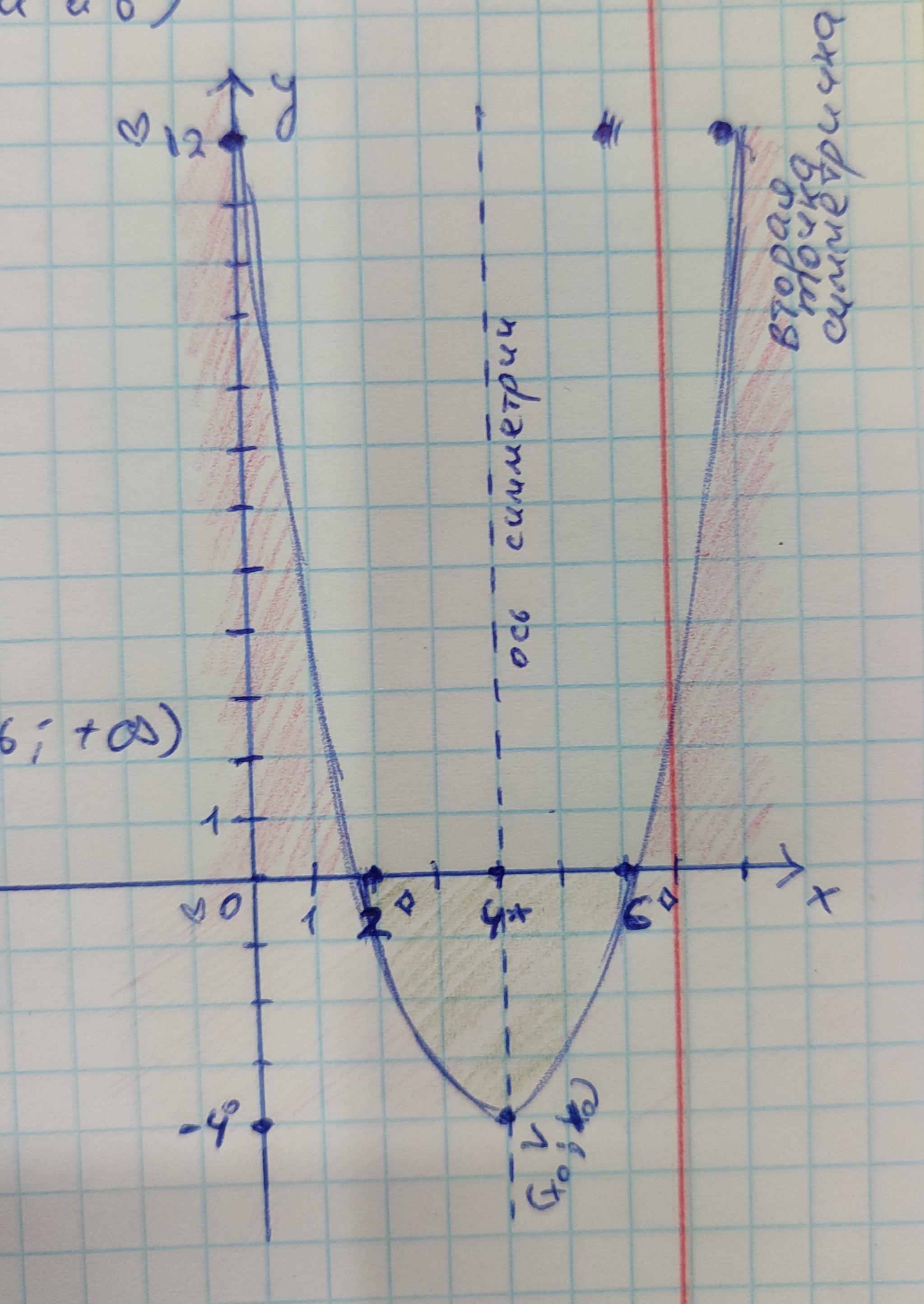
f(x) падает на промежутке (-∞; 4] и возрастает на промежутке [4;+∞)
область значений этой функции равна [f(4); +∞) = [-4; +∞)
Покрокове пояснення:
ax^2 + bx + c; a = 1; b = -8; c = 12
Абсцисса вершины этой параболы равна -b/2a = -(-8)/2*1 = 4; a = 1 > 0 => По свойству параболы, f(x) падает на промежутке (-∞; 4] и возрастает на промежутке [4;+∞).
Поскольку a = 1 > 0, то по свойству параболы – f(4) – min, а следовательно область значений этой функции равна [f(4); +∞) = [-4; +∞)
a > 0 - значит, что парабола направлена "ветками" вверх
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад