Question

Найти площадь полной поверхности усеченной пирамиды.

Answer 1

Ответ:

Площадь полной поверхности пирамиды равна 54+45√3 eд.кв.

Объяснение:

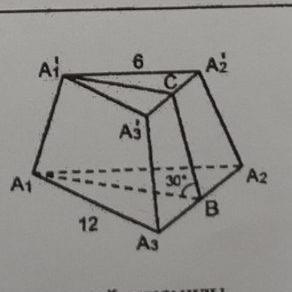
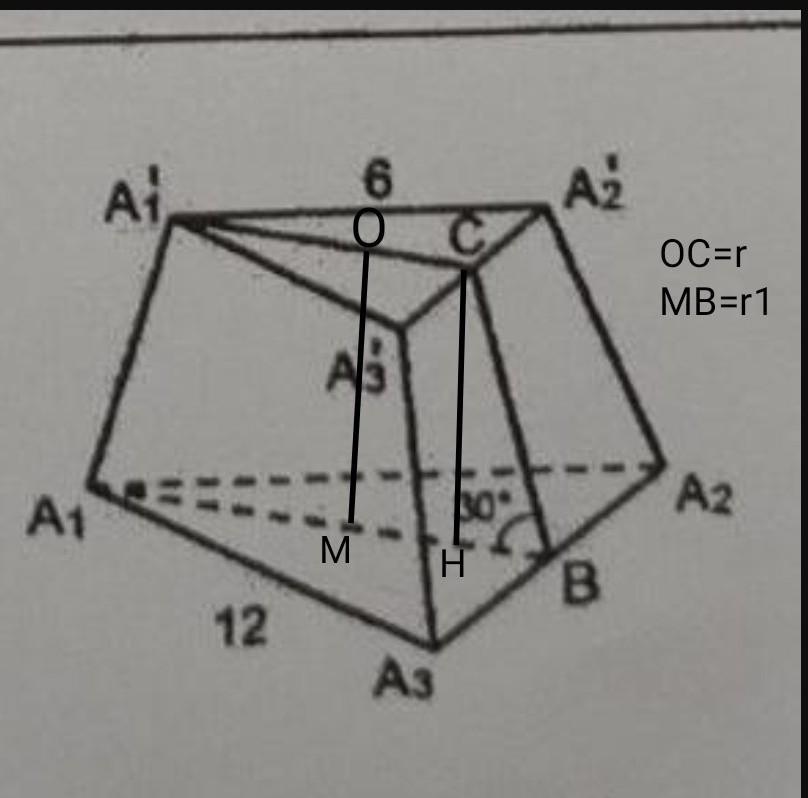
Впишем в основания окружности.

r=ОС; r=A1'A2'/2√3;

OC=6/2√3=√3ед

r1=MB; r1=A1A2/2√3=12/2√3=2√3ед

НВ=MB-OC=2√3-√3=√3ед

∆СНВ- прямоугольный треугольник

cos∠CBH=HB/CB

cos30°=√3/2

√3/2=√3/CB;

CB=2√3/√3=2ед.

Sб=СВ*(Р+Р1)/2;

Р1=3*А1А2=3*12=36ед

Р=3*А1'А2'=3*6=18ед

Sб=2(36+18)/2=54ед.кв.

So=(A1A2)²√3/4=12²√3/4=

=36√3 ед.кв

So2=(A1'A2')²√3/4=6²√3/4=

=9√3ед.кв.

Sп=So+So2+Sб=36√3+9√3+54=

=54+45√3 eд.кв.