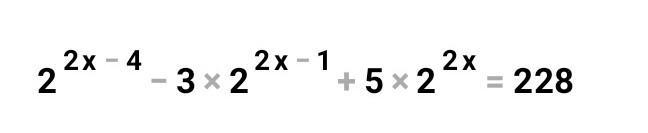Ответы
Ответ дал:
0
Ответ:
13/8
Объяснение:
Для розв'язання рівняння 2^(2x - 4) - 3 * 2^(2x - 1) + 5 * 2^(2x) = 228 використовуйте такий підхід:
Спочатку перепишемо рівняння з умовою:
2^(2x - 4) - 3 * 2^(2x - 1) + 5 * 2^(2x) = 228
Тепер використовуйте правило: a^(m) * a^(n) = a^(m + n).
2^(2x - 4) - 3 * 2^(2x - 1) + 5 * 2^(2x) = 228
Згрупуйте подібні члени:
2^(2x - 4 + (2x - 1) + 2x) = 228
2^(6x - 4 - 1 + 2x) = 228
2^(8x - 5) = 228
Тепер перепишемо 228 як ступінь 2:
2^(8x - 5) = 2^x * 2^x * 2^x * 2^x * 2^x * 2^x * 2^x * 2^x
Так як база (2) однакова, можемо прирівняти показники ступенів:
8x - 5 = 8
Тепер розв'яжемо це рівняння:
8x = 8 + 5
8x = 13
x = 13 / 8
Отже, x = 13/8 є розв'язком цього рівняння. (дріб)
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад