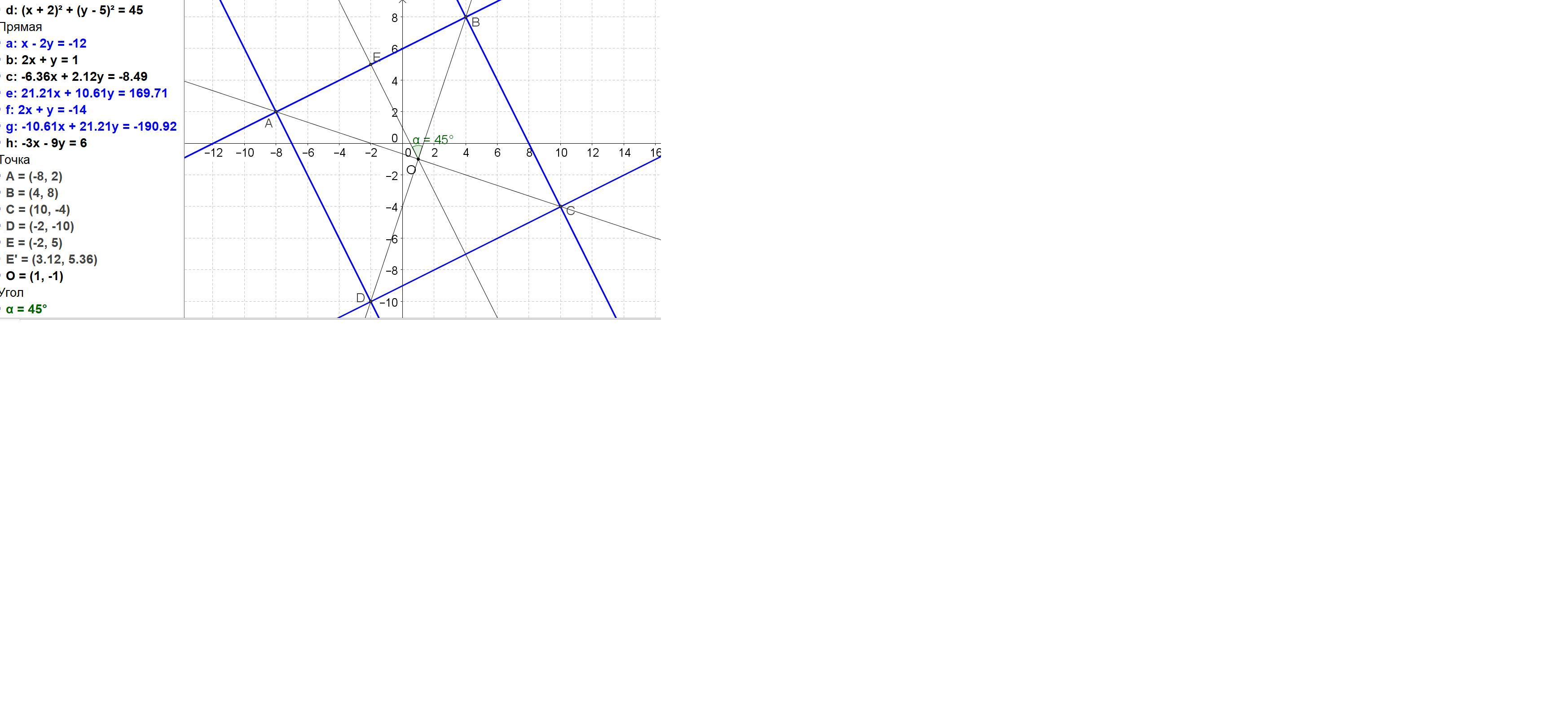
одна из сторон квадрата лежит на прямой x-2y+12=0.Диангонали пересекаются в точке (1,-1).составьте уравнение других сторон квадрата.сделайте чертеж
Ответы
Дано уравнение стороны АВ квадрата x - 2y + 12 = 0 и точка
О(1, -1).
Находим уравнение диагонали ОВ, проходящей под углом 45 градусов к АВ.
Прямая х - 2у + 12 = 0 может быть записана в виде уравнения с угловым коэффициентом: у=kx + b так
2y = x + 12
у = (1/2)х + 6
Значит угловой коэффициент данной прямой
k = (1/2).
Геометрический смысл углового коэффициента:
k = tg α
α– угол наклона прямой у=kx + b c положительным направлением оси Ох.
При пересечении двух прямых
у = k1x + b1 и у = k2x + b2
k1 = tg α1
k2 = tg α2
угол между прямыми
α = α1 – α2
tg α = tg ( α1 + α2)
По формуле тангенса суммы двух углов
tg ( α1+ α2)=(tg α1+ tg α2)/(1 - tg α1·tg α 2)
tg α = tg 45 ° = 1
k = ((1/2))+ 1)/(1- (1/2)·1)
k = (3/2)/(1/2) = 3.
k = 3.
Прямая у = 3х + b проходит через точку O(1; -1).
-1 = 3·1 + b
b = -3 - 1 = - 4.
Получаем уравнение диагонали ОВ: у = 3х – 4 или 3х – у – 4 = 0.
Теперь находим координаты точки В как точки пересечения заданной прямой АВ: x - 2y + 12 = 0 и диагонали ОВ: 3х – у – 4 = 0.
Решаем систему:
{ x - 2y + 12 = 0 x(-3) = -3x + 6y - 36 = 0
{3х – у – 4 = 0 3х – у – 4 = 0
5y – 40 = 0
y = 40/5 = 8.
x = 2y – 12 = 2*8 -12 = 16 – 12 = 4.
Точка В(4; 8).
Уравнение стороны ВС – это перпендикуляр к известной стороне
АВ: x - 2y + 12 = 0.
Используем свойство уравнения перпендикулярной прямой.
Для прямой Ах + Ву + С1 = 0 перпендикулярная прямая имеет такое уравнение: Вх - Ау+ С2 = 0 или -Вх + Ау+ С = 0.
ВС: 2х + у + С = 0.
Подставим координаты точки В(4; 8).
2*4 + 8 + С = 0, отсюда С = -8-8 = -16.
Получаем уравнение стороны ВС: 2х + у - 16 = 0.
Находим уравнение диагонали ОА как перпендикуляра к диагонали ОВ :
3х – у – 4 = 0.
ОА: х + 3у + С = 0, подставим координаты точки О(1; -1).
1 + 3*(-1) + С = 0, отсюда С = 3 – 1 = 2.
Уравнение ОА: х + 3у + 2 = 0.
Теперь находим координаты точки А как точки пересечения заданной прямой x - 2y + 12 = 0 и диагонали ОА: х + 3у + 2 = 0.
Решаем систему:
{ x - 2y + 12 = 0 x(-1) = -x + 2y - 12 = 0
{х + 3у + 2 = 0 х + 3у + 2 = 0
5y – 10 = 0
y = 10/5 = 2.
x = 2y – 12 = 2*2 -12 = 4 – 12 = -8.
Точка A(-8; 2).
В уравнении стороны AD как перпендикуляра к АВ и параллельной стороне ВС коэффициенты при переменных сохраняются.
ВС: 2х + у - 16 = 0
AD: 2х + у + C = 0. Подставим координаты точки А(-8; 2).
2*(-8) + 2 + C = 0, отсюда С = 16 – 2 = 14.
Уравнение стороны AD: 2х + у + 14 = 0.
Находим координаты точки D как точки пересечения стороны
AD: 2х + у + 14 = 0 и диагонали ОВ: 3х – у – 4 = 0.
{2х + у + 14 = 0
{3х – у – 4 = 0
5x + 10 = 0
x = -10/5 = -2,
y = 3x – 4 = 3*(-2) – 4 = -6 - 4 = -10.
Точка D(-2; -10).
В уравнении стороны СD коэффициенты при переменных совпадают с параллельной стороной АВ.
СD: x - 2y + С = 0, подставим координаты точки D(-2; -10).
-2 – 2*(-10) + С = 0, отсюда С = 2 – 20 = -18.
Уравнение стороны СD: х - 2у -18 = 0.