Question

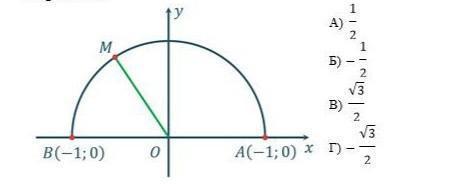
Одиничному колу належить точка M(−1/2
;√3/2). Тоді sin MOA дорівнює:
А)1/2
Б)−1/2
В)√3/2
Г)−√3/2

Answer 1

Ответ:

B) √3/2

Объяснение:

Одиничному колу належить точка M(−1/2; ;√3/2). Тоді sin MOA дорівнює?

На осі 0у (ординат) одиничного кола відкладають значення синусів.

Ордината точки М: √3/2.

Маємо синус ∠МОА:

sin∠MOA = √3/2.

Відповідь: В.

#SPJ1