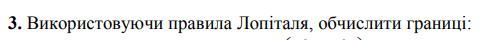Ответы
Ответ дал:
2
Ответ:
Правило Лопиталя применяется при раскрытии неопределённостей
вида 0/0 и ∞/∞ .
Применяем правило Лопиталя в 1 примере 3 раза .
fctdgsygfdhngfxzgsac:
спасибо большое)
здравствуйте, извините за беспокойство, можете помочь пожалуйста
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад