12y^2 - 12x - 32y - 29 = 0 Найти канонический вид( это парабола я так понимаю) и характеристики. Пожалуйста!
Ответы
Ответ дал:
1
Ответ:
Парабола .
Приведём к каноническому виду , выделив полный квадрат .
По каноническому виду параболы делаем заключение, что
- ветви параболы направлены вправо ,
- вершина параболы находится в точке
ось симметрии параболы - прямая ,
- параметр равен ,
- фокус находится в точке
,
- уравнение директрисы -
Приложения:

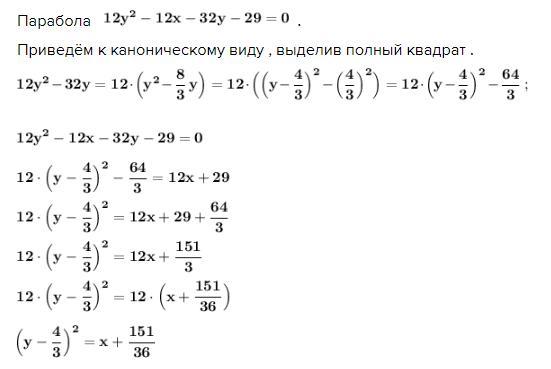

masha01021:
здравствуйте NNNNL54, если у вас будет время посмотрите пожалуйста, у меня сложнач задача
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
8 лет назад