Question

Обчислити площу фігури обмеженої лініями у=х^2-6х+8 і у=-2х^2+12х-16

Answer 1

Ответ:     4 кв.ед.

Пошаговое объяснение:

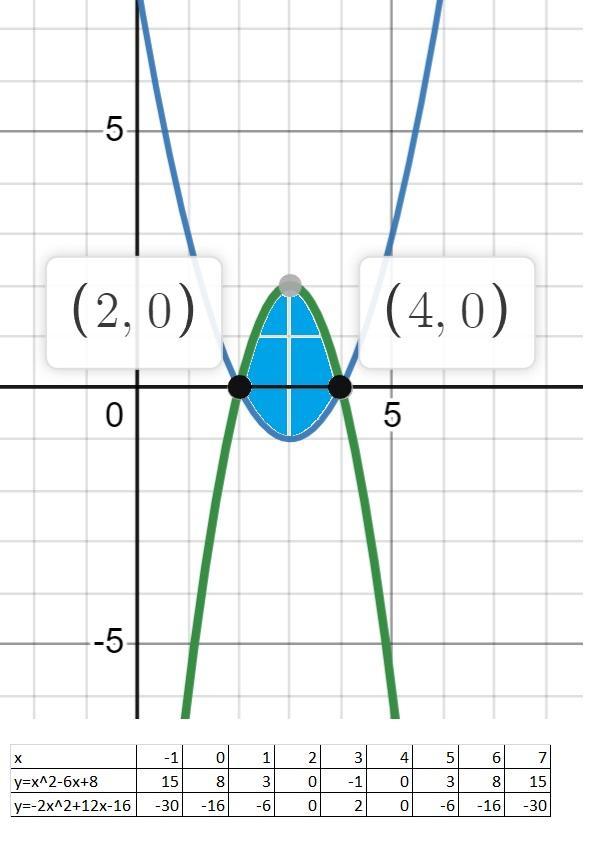
Строим графики функций у=х^2-6х+8; у=-2х^2+12х-16.

Площадь S=∫(a;b)f₁(x)dx - ∫(a;b)f₂(x)dx, где

Пределы интегрирования a=2;  b=4.

f₁(x) = -2х^2+12х-16.

f₂(x) = у=х^2-6х+8. Тогда

S=∫(2;4) (-2х^2+12х-16)dx - ∫(2;4) (х^2-6х+8) dx = 8/3*(-4/3) = 12/3 = 4кв.ед.

-------------

1)  ∫(2;4) (-2x^2) + ∫(2;4) (12x)dx - ∫(2;4)(16)dx =

=-2/3(x^3)|(2;4) + 12/2(x^2)|(2;4) - 16(x)|(2;4) =

= -2/3(4^3-2^3) + 6(4^2-2^2) - 16(4-2) =

= -2/3(64-8)+6(16-4)-16*2 = -2/3 *56 + 6*12 - 32 =  8/3;

--------------

2)  ∫(2;4)(x^2)dx + ∫(2;4)(6x)dx - ∫(2;4)(8)dx  =

= 1/3(x^3)|(2;4) - 6/2(x^2)|(2.4) + 8(x)|(2;4) =

=  1/3(4^3-2^3) - 3(4^2-2^2) + 8(4-2) = 1/3(64-8) - 3(16-4) + 8*2 =

=  1/3 *56 - 3*12 + 16 = -4/3.