Ответы
Объяснение:
7.
а)
∠MKE=∠EKP ,т.к КЕ - биссектриса
∠ЕКР=∠МЕК - как накрест лежащие при
КР||МN и секущей КЕ , значит
∠МКЕ=∠МЕК , следовательно,∆КМЕ - равнобедреный.
КМ=МЕ=10 см.
Р(КМNP)=2(KM+KP)
KP=Р/2 - КМ=52/2 - 10=16 см
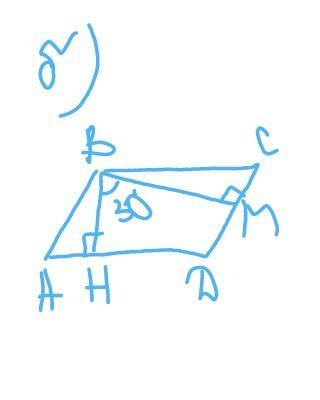
б)
АВСD - параллеллограмм ; АВ=СD=10 см ;
АD=BC=20 см ; ВН и ВМ - высоты ;
∠НВМ=30°
найти: ВН+ВМ
решение:
угол между высотами параллеллограмма ,проведенными из вершины тупого угла равен острому углу параллелограмма, значит ∠А=∠С=30°.
Катет лежащий против угла 30° равен половине гипотенузы.
∆АВН - прямоугольный:
ВН=АВ:2=10:2=5 см
∆ВМС - прямоугольный :
ВМ=ВС:2=20:2=10 см
ВН+ВМ=5+10=15 см
в)
Медиана треугольника - отрезок в треугольнике ,соединяющий вершину треугольника с серединой стороны, противопложной этой вершине.
В прямоугольнике диагонали точкой пересечения делятся пополам,значит
АО=ОС , следовательно, ВО является медианой ∆АВС.
г)
∠AFD=180-∠AFC=180-120=60°
∆АDF -прямоугольный:
∠FAD=90-∠AFD=90-60=30°
FD=CD:2=6:2=3 см
Катет лежащий против угла 30° равен половине гипотенузы: АF=2•FD=2•3=6 см.
∆СВО=∆АDF - по 2 катетам ,значит
ОC=АF=6 см.
АО=АВ:2=СD:2=6:2=3 см
Р(АОСF)=АО+ОС+СF+AF=
=3+6+3+6=18 см