Question

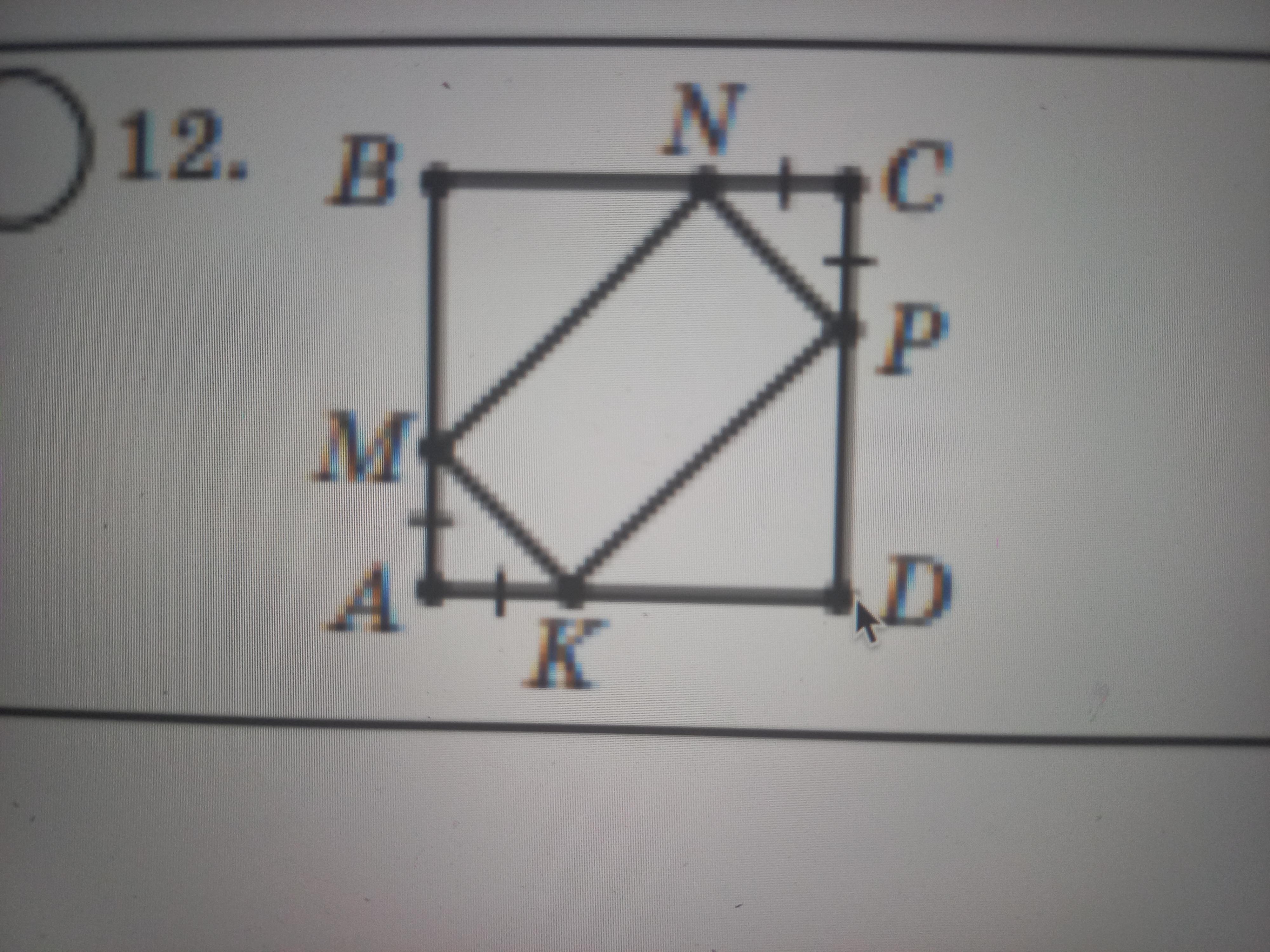
На сторонах квадрата ABCD поставлено точки М. N. Р. К так, як показано на рисунку. AM = AK = CN = CP Чотирикутник MNPK є

Answer 1

ABCD - квадрат:

все углы прямые, ∠A=B=C=D=90°

все стороны равны, AB=BC=CD=AD

△MAK - равнобедренный прямоугольный.

В равнобедренном треугольнике углы при основании равны.

В прямоугольном треугольнике сумма острых углов 90°.

=> ∠AMK=AKM =90/2 =45°

BM =AB-AM =BC-CN =BN

△MBN - равнобедренный прямоугольный => ∠BMN=BNM=45°

Аналогично ∠CNP=∠CPN=45° (△NCP); ∠DPK=∠DKP=45° (△PDK)

∠KMN=180°-∠AMK-∠BMN =180°-45°-45° =90°

Аналогично ∠MNP, ∠NPK, ∠PKM - прямые углы.

MNPK - прямоугольник.