Ответы
Відповідь:
Пояснення:


Ответ:
Объяснение:
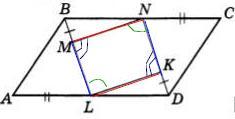
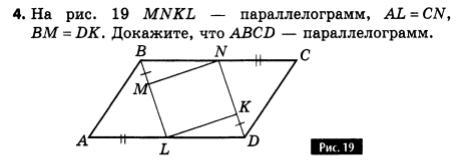
1. Рассмотрим ΔВМТ и ΔDKL.
1) ВМ = KD по условию
2) MN = LK как стороны параллелограмма LMND.
3) ∠BMN смежный с ∠LMN, а
∠DKL смежный с ∠LKN;
Сумма смежных углов = 180°.
Учитывая, что противоположные углы параллелограмма
равны, т.е. ∠LMN = ∠LKN то и
∠BMN = ∠DKL
4) ΔВМТ = ΔDKL по двум сторонам и углу между ними (1-ый
признак равенства Δ-ков), следовательно, и
BN = LD, ∠BNM = ∠KLD
2. AL = NC по условию, LD =BN, значит,
AD = BC
3. Рассмотрим ΔABL и ΔCDN.
AL = NC по условию
BL = ND, т.к. BM = DK по условию и ML = KN как противоположные
стороны параллелограмма.
∠ALB = 180° - ∠MLK - ∠KLD (развернутый угол = 180°)
∠CND = 180° - ∠MNK - ∠BNM
Но т.к. ∠MLK = ∠MNK(противоположные углы параллелограмма) и
∠KLD = ∠BNM, то и
∠ALB = ∠CND
Т.о., AL = NC, BL = ND, ∠ALB = ∠CND.
ΔABL = ΔCDN по 2-м сторонам и углу между ними (1-ый признак равенства Δ-ков). Тогда и
AB = DC
3. AD = BC, AB = DC, следовательно, ABCD - параллелограмм
(Если в четырехугольнике противолежащие стороны попарно равны, то этот четырехугольник — параллелограмм).