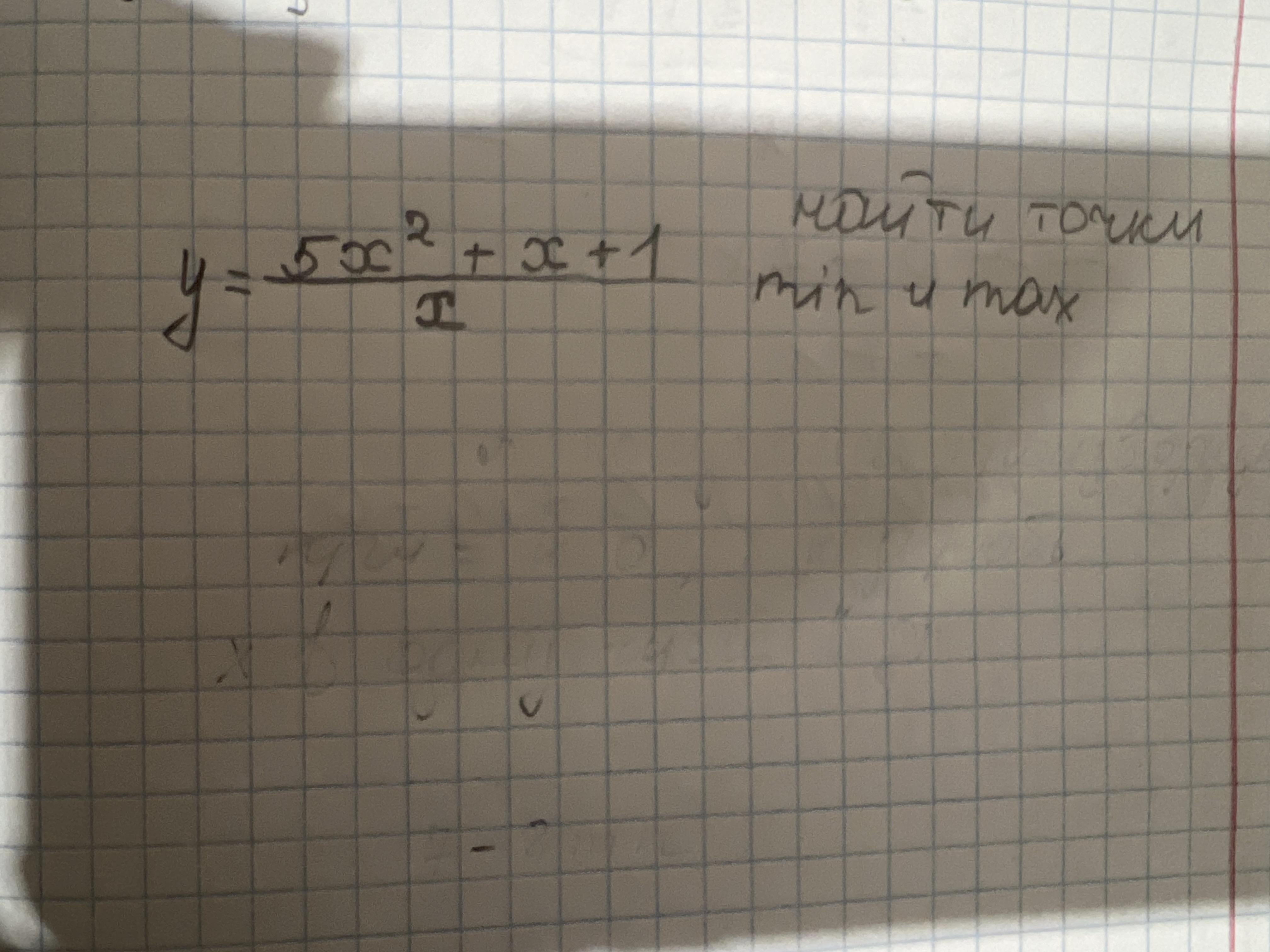Question

Помогите даю 80 баллов
Найти точки min u max y=5x^2+x+1/x

Answer 1

Ответ:

$\tt \displaystyle x_1=-\frac{1}{\sqrt{5} }$  - точка максимума, $\tt \displaystyle x_2=\frac{1}{\sqrt{5} }$ - точка минимума

Объяснение:

Информация. Для того, чтобы найти точку минимума и максимума функции нужно:

1) приравнять производную функции к нулю, найти значения переменной полученного выражения, то есть найти критических точек;

2) разбить критическими точками координатную прямую и вычислить, какие из полученных отрезков будут положительным, а какие - отрицательными;

3) среди критических точек найти точку, в которой значение производной сменяется с минуса на плюс - это точка минимума, значение производной сменяется с плюса на минус - это точка максимума.

Решение. Находим производную от функции в области определения функции, то есть при x∈(-∞; 0) ∪ (0; +∞). :

$\tt \displaystyle y'= \bigg (\frac{5 \cdot x^2+x+1}{x} \bigg )'=\bigg (5 \cdot x+1+\frac{1}{x} \bigg )'=(5 \cdot x)'+(1)'+(x^{-1})'= \\\\=5+0+(-1) \cdot (x^{-1-1})=5-\frac{1}{x^2}.$

1) Приравниваем производную от функции к нулю и решим уравнение:

$\tt \displaystyle y'= 0 \Leftrightarrow 5-\frac{1}{x^2}=0 \Leftrightarrow x^2=\frac{1}{5} \Leftrightarrow x_1=-\frac{1}{\sqrt{5} } , \; x_2=\frac{1}{\sqrt{5} }.$

2) Критические точки делят ось Ох на интервалы:

$\tt \displaystyle (-\infty; -\frac{1}{\sqrt{5} }) , \; (-\frac{1}{\sqrt{5} };0),\; (0; \frac{1}{\sqrt{5} }), \; (\frac{1}{\sqrt{5} };+\infty).$

3) Определим знаки производной на каждом из интервалов:

$\tt \displaystyle -1 \in (-\infty; -\frac{1}{\sqrt{5} }) :y'(-1)=5-\frac{1}{(-1)^2} =5-1=4 > 0;$

$\tt \displaystyle -\frac{1}{3} \in (-\frac{1}{\sqrt{5} };0): y'(-\frac{1}{3} )=5-\frac{1}{(-\frac{1}{3} )^2} =5-\frac{1}{\frac{1}{9} } =1-9=-8 < 0;$

$\tt \displaystyle \frac{1}{3} \in (0; \frac{1}{\sqrt{5} }): y'(\frac{1}{3} )=5-\frac{1}{(\frac{1}{3} )^2} =5-\frac{1}{\frac{1}{9} } =1-9=-8 < 0;$

$\tt \displaystyle 1 \in (\frac{1}{\sqrt{5} };+\infty):y'(1)=5-\frac{1}{1^2} =5-1=4 > 0.$

Значит, производная меняет знак с плюса на минус при переходе через точку $\tt \displaystyle x_1=-\frac{1}{\sqrt{5} }$  - точка максимума, с минуса на плюс при переходе через точку $\tt \displaystyle x_2=\frac{1}{\sqrt{5} }$ - точка минимума.

#SPJ1