Question

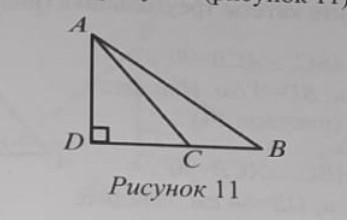
40. в тупоугольном треугольнике ABC, AD перпендикулярно BC, AB=16√2 см, ВС=4 см, угол B=45°. найдите сторону AC.
Пожалуйста решите дам много много баллов ​

Answer 1

Объяснение:

1 способ :

∆АВС :

из теоремы косинусов:

АС=√(АВ²+ВС²-2•АВ•ВС•соsB)=

=√((16√2)²+4²-2•(16√2)•4•cos45)=

=√(512+16-2•16√2•4•√2/2)=√400=20 см

ответ: АС=20 см

или

2 способ:

∆АDB - прямоугольный:

сумма острых углов в прямоугольном тр-ке равна 180°

∠DAB=90-∠B=90-45=45°

∆АDB - равнобедреный: АD=DB.

Пусть DC=х см , тогда

DB=DC+BC=(x+4) cм

АD=DB=(x+4) см

по теореме Пифагора:

АD²+DB²=AB²

(x+4)²+(x+4)²=(16√2)²

x²+8x+16+x²+8x+16=512

2x²+16x+32=512

2x²+16x+32-512=0

2x²+16x-480=0

x²+8x-240=0

D=64-4•1•(-240)=1024

x1=(-8-32)/2= -20 не подходит

х2=(-8+32)/2=12 см

DC=12 см

AD=DB=12+4=16 см

∆АDC - прямоугольный:

по теореме Пифагора:

АС=√(АD²+DC²)=

=√(16²+12²)=√400=20 см

ответ: АС=20 см