Question

ПЖ СРОЧНО!!!
Трапеція вписана в коло так, що діаметр кола є більшою основою трапеції, а менша основа дорівнює біч ній стороні. Знайдіть периметр трапеції, якщо діаметр кола дорівнює 18 см.​

Answer 1

Відповідь:

45 (см)

Пояснення:

1) У коло може бути вписана тільки рівнобічна трапеція.

За умовою так  як трапеція рівнобічна маємо:

АВ=ВС=СD.

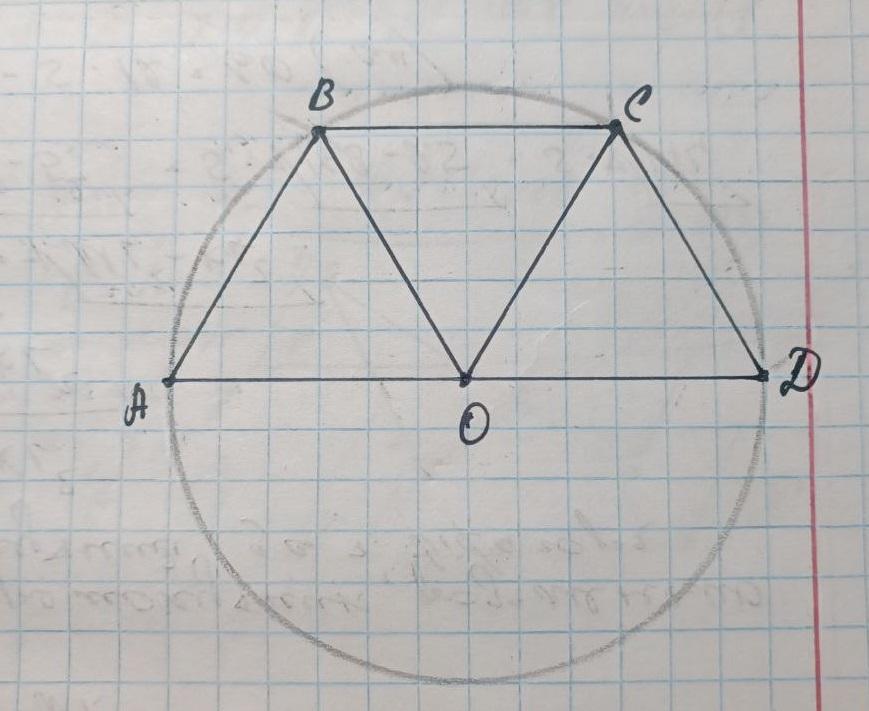
2) Розглянемо три трикутника Δ АОВ, Δ ВОС та Δ СОD:

ОА=ОВ=ОС=ОD як радіуси,

АВ=ВС=СD за умовою,

Отже:

Δ АОВ, Δ ВОС та Δ СОD - рівні за трима сторонами.

3) ∠АОВ = ∠ВОС = ∠СОD за п.2

∠АОD розгорнутий і рівен 180°,

отже кути АОВ = ∠ВОС = ∠СОD=180°/3=60°.

Так як трикутники Δ АОВ, Δ ВОС та Δ СОD рівнобедрені з кутом при вершині 60°, маємо що кути при основі (180°-60°)/2=60°, а отже вони рівносторонні.

4) за умови d= 18 см. отже r=d/2=9 (см),

а периметр трапеції рівен Р= 5r = 5 * 9 = 45 (см)