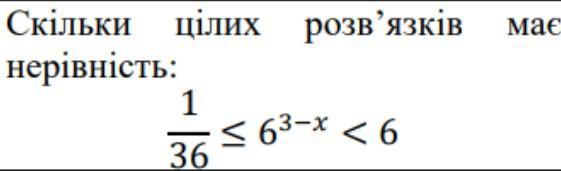Ответы
Ответ:
безкінечно
Пошаговое объяснение:
Для того, чтобы найти цілі розв'язки даної нерівності, спочатку спробуємо спростити її.
Почнемо з першої нерівності:
\[
\frac{1}{36} \leq 6^{3-x}
\]
Ми можемо записати числову основу 6 у вигляді дробу з цілочисельним основою 6:
\[
\frac{1}{36} \leq \left(\frac{6}{6}\right)^{3-x} = \left(\frac{6}{6}\right)^3 \cdot \left(\frac{6}{6}\right)^{-x} = \frac{216}{6^x}
\]
Тепер ми маємо:
\[
\frac{1}{36} \leq \frac{216}{6^x}
\]
Далі, спрощуємо другу нерівність:
\[
6^{3-x} < 6
\]
Аналогічно, записуємо числову основу 6 як дріб:
\[
\left(\frac{6}{6}\right)^{3-x} < \frac{6}{6} = 1
\]
Отримуємо:
\[
\frac{216}{6^x} < 1
\]
Тепер ми маємо систему нерівностей:
\[
\frac{1}{36} \leq \frac{216}{6^x} < 1
\]
Щоб вирішити цю систему нерівностей, спочатку зважаємо на першу нерівність:
\[
\frac{1}{36} \leq \frac{216}{6^x}
\]
Можна помножити обидві частини нерівності на $36 \cdot 6^x$:
\[
1 \cdot 6^x \leq 36 \cdot 216
\]
Отримуємо:
\[
6^x \leq 7776
\]
Тепер звернемо увагу на другу нерівність:
\[
\frac{216}{6^x} < 1
\]
Можна помножити обидві частини нерівності на $6^x$:
\[
216 < 6^x
\]
Зараз ми маємо дві нерівності:
\[
\begin{cases}
6^x \leq 7776 \\
216 < 6^x
\end{cases}
\]
Для першої нерівності $6^x \leq 7776$, ми можемо помітити, що $6^2 = 36$ і $6^3 = 216$, тому ця нерівність має розв'язок $x \leq 3$.
Для другої нерівності $216 < 6^x$, ми бачимо, що $6^3 = 216$, тому ця нерівність має розв'язок $x > 3$.
Отже, система нерівностей має розв'язок $x \in (3, \infty)$.
Отже, нерівність має нескінченну кількість цілих розв'язків.