Question

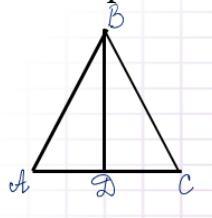
В трикутнику ABC, медіана BD перпендикулярна до сторони АС. довести що АВ = ВС
СРОЧНОООООООООООООО ПОМОГИТЕЕЕЕЕЕЕЕЕ
ДАЮ 40 БАЛОООООООООООВ

Answer 1

Давайте розглянемо трикутник ABC, де медіана BD перпендикулярна до сторони AC.

Ми знаємо, що медіана поділяє сторону від вершини трикутника на дві рівні частини. Тобто, BD = CD.

Також, оскільки медіана перпендикулярна до сторони AC, то ми можемо сказати, що трикутник ABD - прямокутний трикутник.

Отже, за теоремою Піфагора в прямокутному трикутнику ABD:

$AB^{2} + BD^{2} = AD^{2}$

Аналогічно, за теоремою Піфагора в прямокутному трикутнику CBD:

$BC^{2} + CD^{2} = BD^{2}$

Оскільки BD = CD (оскільки BD - медіана), ми можемо прирівняти обидві рівності:

$AB^{2} + BD^{2} = BC^{2} + CD^{2}$

З урахуванням BD = CD, ми отримуємо:

$AB^{2} = BC^{2}$

Це означає, що сторони AB і BC рівні між собою: AB = BC.

Таким чином, ми довели, що в трикутнику ABC, якщо медіана BD перпендикулярна до сторони AC, то AB = BC.