Question

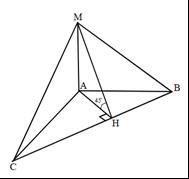
Дано: ABC – рівнобедрений трикутник, AM перпендикулярно (ABC), MH перпендикулярно BC,

AB = 10, BC = 12, ∠MHA = 45°, (рисунок).
Потрібно знайти:
1) відстань від точки M до сторони ВС
2) площа трикутника MBC
3) площа трикутника MHA
4) довжина похилої MC
5) довжина перпендикуляра МА
6) тангенс кута нахилу похилої МС до площини (ABC)

Answer 1

Ответ:

1) Відстань від точки M до сторони BC можна знайти, використовуючи трикутник AMH та властивість подібних трикутників. Знаючи, що AM перпендикулярне BC та ∠MHA = 45°, можемо визначити цю відстань.

2) Площа трикутника MBC може бути обчислена, використовуючи півпериметр і радіус вписаного кола, оскільки MBC - рівнобедрений трикутник.

3) Площу трикутника MHA можна знайти як половину добутку сторін AB та MH.

4) Довжина похилої MC може бути знайдена за допомогою теореми Піфагора у трикутнику MBC.

5) Довжина перпендикуляра MA може бути знайдена використовуючи піфагорівський трикутник AMH.

6) Тангенс кута нахилу похилої MC до площини ABC можна знайти, розділивши висоту M до BC на відстань від M до точки дотику похилої до площини.