Question

У рівнобедреному трикутнику кут між бічною стороною основою дорівнює 30°, а бічна сторона 12 см. Знайти основу трикутника, якщо його площа дорівнює
60 см. Будь ласка з поясненням. Даю багато балів.

Answer 1

Ответ:

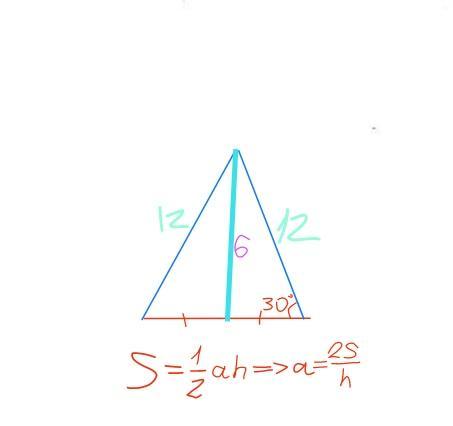
Якщо ми проведемо висоту до основи трикутника, то отримаємо 2 прямокутні рівні трикутники за 2 ознакою рівність трикутників, бо висота в рівнобедреному трикутнику, це медіана і бісектриса кута. Тому основа трикутника поділена на 2 однакові частини за ознакою медіани, тому ці два трикутники рівні.

Нижче зобразив схематичне зображення цього трикутника. Проти кута в 30° лежить катет, який у 2 рази менший за гіпотезу. Гіпотенузою є бічна сторона трикутника, яка з умови дорівнює 12 см. А сторона, яка лежить проти катета в 30° це висота. Тому висота дорівнює 12:2=6 (см)

Тепер ми можемо знайти основу трикутника з формули площі трикутника. аh×1/2=S=>ah=2S=>a=2S/h

a=60×2/6=20 (см)

Відповідь: 20 см