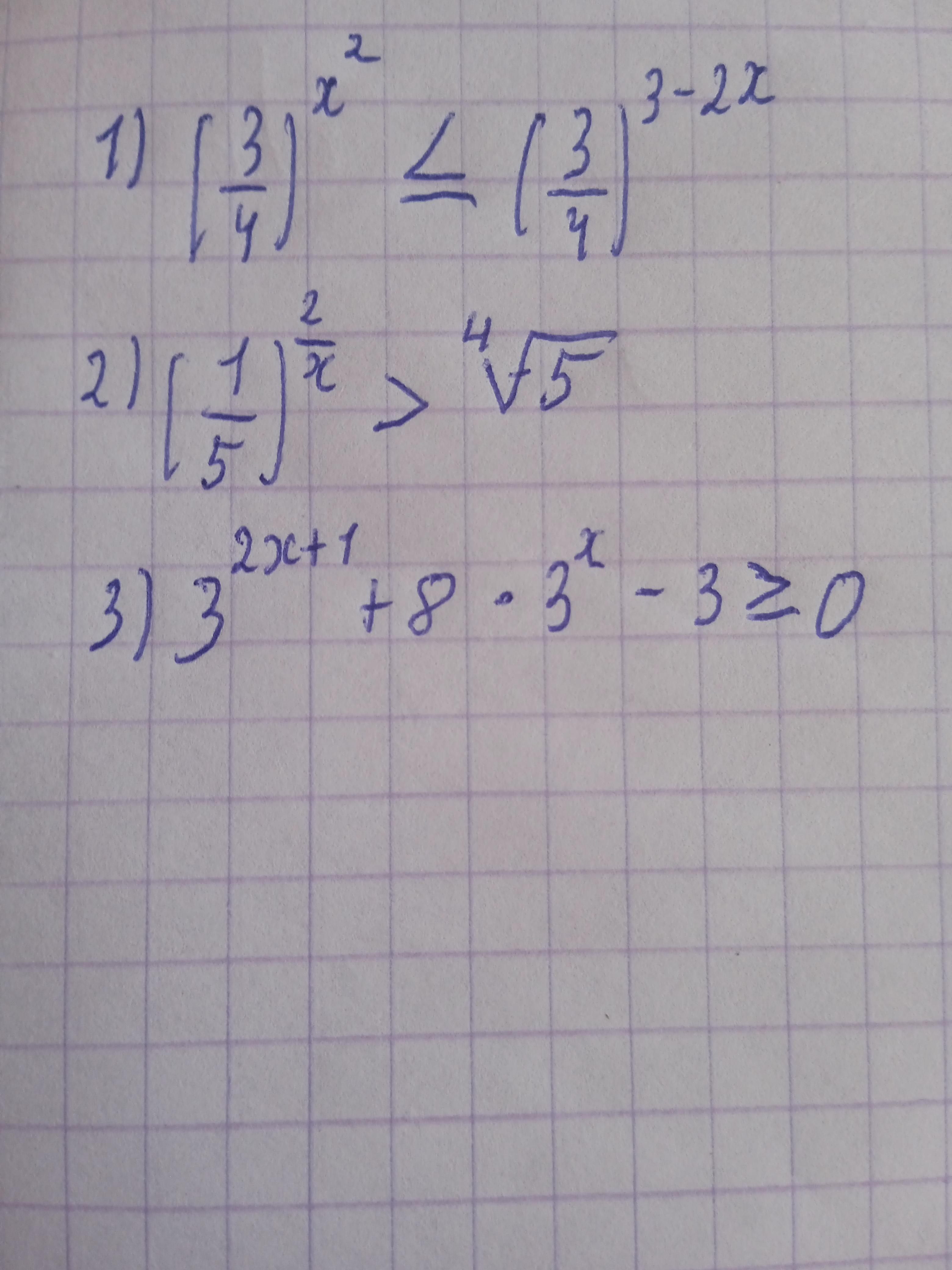Question

ДАЮ СТО БАЛЛОВ

ЗАДАНИЕ НЕ СЛОЖНОЕ ВРОДЕ
СРОЧНО

Знайдіть розв'язки нерівностей:

Answer 1

Ответ:

1) x ∈ (-∞; -3) ∪ (1; +∞)

2) x ∈ (-8; 0)

3) x ∈ [-1; +∞)

Объяснение:

Требуется решить неравенства.

Информация. Решение простых показательных неравенств:

$\tt 1) \; a^b < a^c, \; a > 1 \Leftrightarrow b < c; \\\\ 2) \; a^b < a^c, \; 0 < a < 1 \Leftrightarrow b > c.$

Решение. Преобразуем неравенства и решим простые показательные неравенства.

$\tt 1) \; \bigg (\dfrac{3}{4} \bigg )^{x^2} \leq \bigg (\dfrac{3}{4} \bigg )^{3- 2 \cdot x} \\\\0 < \dfrac{3}{4} < 1:\\\\x^2 \geq 3- 2 \cdot x \\\\x^2+2 \cdot x-3 \geq 0 \\\\x^2+3 \cdot x-x-3 \geq 0 \\\\(x+3) \cdot x-(x+3) \geq 0\\\\(x+3) \cdot (x-1) \geq 0 \\\\x \in (-\infty; -3) \cup (1; +\infty).$

$\tt 2) \; \bigg (\dfrac{1}{5} \bigg )^{\dfrac{2}{x} } > \sqrt[4]{5} \\\\ \bigg (5^{-1} \bigg )^{\dfrac{2}{x} } > 5^{\dfrac{1}{4} }\\\\ 5^{-\dfrac{2}{x} } > 5^{\dfrac{1}{4} }, \; 5 > 1 \\\\-\dfrac{2}{x} > \dfrac{1}{4} \\\\\dfrac{1}{4} +\dfrac{2}{x} < 0 \\\\\dfrac{x+8}{4 \cdot x} < 0 \\\\x \in (-8;0).$

$\tt 3) \; 3^{2 \cdot x+1}+8 \cdot 3^x-3 \geq 0 \\\\3 \cdot 3^{2 \cdot x}+8 \cdot 3^x-3 \geq 0 , t=3^x > 0 \\\\3 \cdot t^{2}+8 \cdot t-3 \geq 0 \\\\3 \cdot t^{2}+9 \cdot t-t-3 \geq 0 \\\\3 \cdot t \cdot (t+3) -(t+3) \geq 0 \\\\(3 \cdot t -1) \cdot (t+3) \geq 0 \\\\(t -\dfrac{1}{3} ) \cdot (t+3) \geq 0 \\\\t \geq \dfrac{1}{3} \lor t \leq -3, \; t > 0$

$\tt t \geq \dfrac{1}{3} , \; t=3^x \\\\3^x \geq \dfrac{1}{3} \\\\3^x \geq 3^{-1}, \; 3 > 1 \\\\x \geq -1 \\\\x \in [-1; +\infty).$

#SPJ1