Ответы
Ответ дал:
1
Ответ:
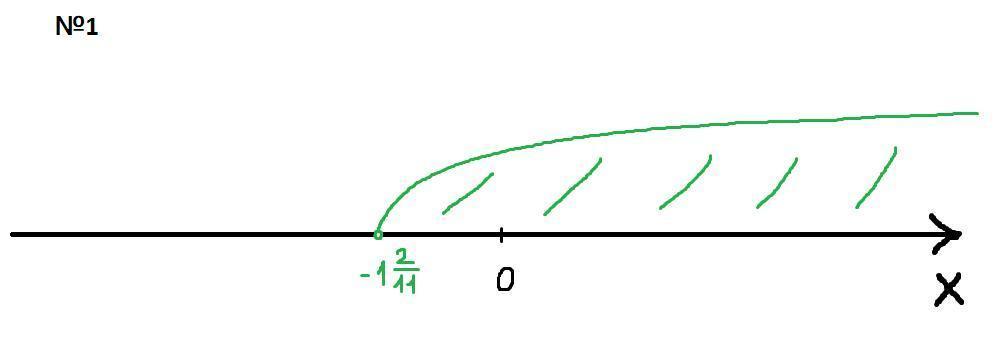
1) невозможно найти наибольший целый корень, так как корней больше ноля бесконечное количество
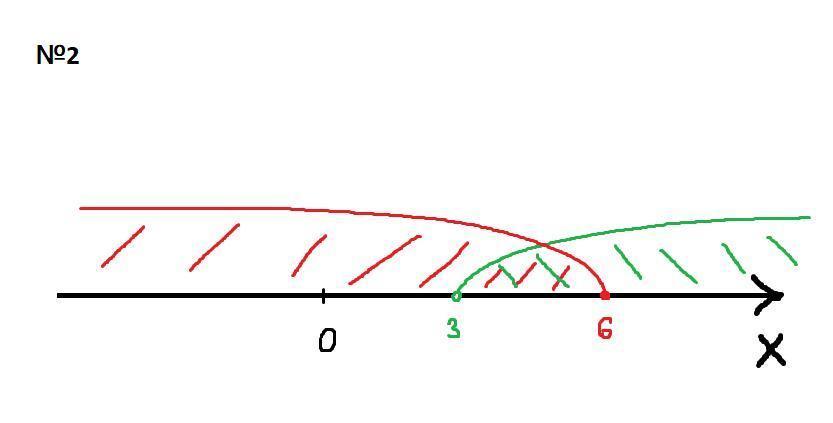
2) x ∈ (3; 6]
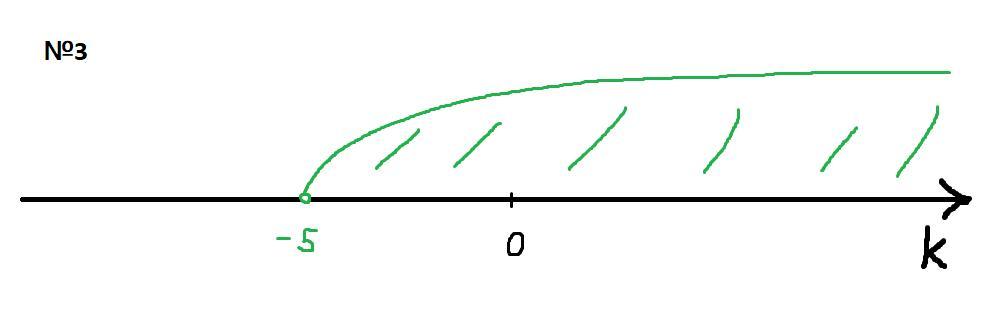
3) k > -5
Объяснение:
№1
(Либо в задании опечатка, либо задача с подвохом)
Ответ: невозможно найти наибольший целый корень, так как корней больше ноля бесконечное количество
№2
№3
— два корня
Ответ: уравнение имеет два корня при
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
