Ответы
Ответ дал:
0
Ответ:
Найти значения a , b , c , при которых являются тождествами заданные равенства .
Получим тождество : .
Получим тождество :
Приложения:
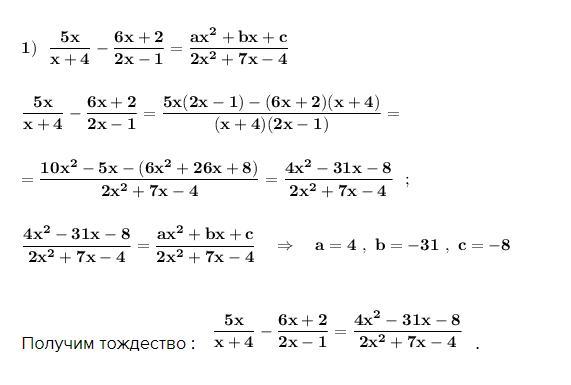

Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад
