Question

Помогите пожалуста СРОЧНО!! Задание на фото. ЧЕРЕЗ ДАНО. Даю 50б​

Answer 1

Объяснение:

дано

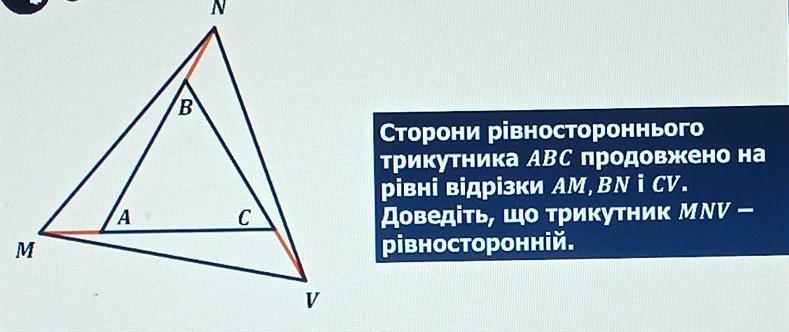
АВС- равносторонний: АВ=ВС=АС=x

АМ=ВN=CV=y

Доказать : ∆МNV - равносторонний:

∆АВС: ∠А=∠В=∠С=α

рассмотрим ∆МАN ; ∆NBV ; ∆VCM :

AN=AB+BN=x+y

BV=BC+CV=x+y

MC=AC+AM=x+y

||

✓

АN=BV=MC

∠MAN=180-∠A=180-α - как смежные

∠NBV=180-∠B=180-α - как смежные

∠VCM=180-∠С=180-α - как смежные

||

✓

∠МАN=∠NBV=∠VCM

AM=BN=CV - по условию

∆МАN=∆NBV=∆VBM по 2 сторонам и углу между ними, значит МN=NV=MV , следовательно, ∆МNV - равносторонний,что и требовалось доказать.