Question

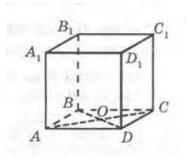
Дано куб ABCDA1B1C1D1, точка O - центр грани ABCD, укажите угол между

1)прямой AB1 ​​и плоскостью A1B1C1;
2) прямой AC1 и плоскостью ABC;
3) прямой AC1 и плоскостью CDD1;
4) прямой OA1 и плоскостью ABC;
5) прямой AC и плоскостью ADD1;

Answer 1

1) Угол между прямой и плоскостью - угол между прямой и ее проекцией.

Из концов отрезка опускаем перпендикуляры на плоскость - получаем проекцию.

AA1⊥(A1B1C1) (ребро куба перпендикулярно основанию)

A1 - проекция A на (A1B1C1)

A1B1 - проекция AB1 на (A1B1C1)

∠(AB1;A1B1C1) =∠(AB1;A1B1) =∠AB1A1 =45° (диагональ квадрата -биссектриса прямого угла)

2) ∠(AC1;ABC) =∠(AC1;AC) =∠C1AC

Пусть ребра куба равны 1

СС1=1, AC=√2 (диагональ квадрата)

tg(C1AC)=CC1/AC =1/√2

∠C1AC =arctg(1/√2)

3) ∠(AC1;CDD1)=∠(AC1;DC1)=∠AC1D=arctg(AD/DC1)=arctg(1/√2)

4) OA=1/√2

∠(OA1;ABC)=∠(OA1;OA)=∠A1OA=arctg(AA1/OA)=arctg(√2)

5) ∠(AC;ADD1)=∠(AC;AD)=∠CAD=45°